题目内容
6.函数$y=sin(-2x+\frac{π}{6})$的单调递减区间是[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z.分析 由条件利用诱导公式、正弦函数的单调性,求得函数$y=sin(-2x+\frac{π}{6})$的单调递减区间.
解答 解:对于函数$y=sin(-2x+\frac{π}{6})$=-sin(2x-$\frac{π}{6}$),令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,
求得kπ-$\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$,故函数的减区间为[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z,
故答案为:[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z.
点评 本题主要考查诱导公式、正弦函数的单调性,属于基础题.

练习册系列答案
相关题目
11. 如图,在底面为平行四边形的棱柱ABCD-A1B1C1D1中,AB=AD=2AA1=2,且∠A1AB=∠A1AD=∠BAD=60°,则四棱柱ABCD-A1B1C1D1的对角线AC1的长为( )
如图,在底面为平行四边形的棱柱ABCD-A1B1C1D1中,AB=AD=2AA1=2,且∠A1AB=∠A1AD=∠BAD=60°,则四棱柱ABCD-A1B1C1D1的对角线AC1的长为( )
 如图,在底面为平行四边形的棱柱ABCD-A1B1C1D1中,AB=AD=2AA1=2,且∠A1AB=∠A1AD=∠BAD=60°,则四棱柱ABCD-A1B1C1D1的对角线AC1的长为( )
如图,在底面为平行四边形的棱柱ABCD-A1B1C1D1中,AB=AD=2AA1=2,且∠A1AB=∠A1AD=∠BAD=60°,则四棱柱ABCD-A1B1C1D1的对角线AC1的长为( )| A. | $\sqrt{14}$ | B. | 4 | C. | $\sqrt{17}$ | D. | $\sqrt{19}$ |
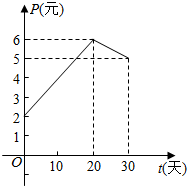 某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40-t(0≤t≤30且t∈N).
某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40-t(0≤t≤30且t∈N).