题目内容
11.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点分别为F1、F2,在双曲线C上存在点P,满足△PF1F2的周长等于双曲线C的实轴长的3倍,则双曲线C的离心率的取值范围是( )| A. | (1,$\frac{3}{2}$) | B. | (0,$\frac{3}{2}$) | C. | (1,$\frac{5}{2}$) | D. | (0,$\frac{5}{2}$) |
分析 可设P为双曲线的右支上一点,|PF1|=m,|PF2|=n,运用双曲线的定义和P在右支上,有n>c-a,结合不等式的性质和离心率公式计算即可得到所求范围.
解答 解:可设P为双曲线的右支上一点,
|PF1|=m,|PF2|=n,
由双曲线的定义可得m-n=2a,
由题意可得m+n+2c=6a,
即有2n+2a+2c=6a,
即n=2a-c,
再由P在右支上,可得n>c-a,
即有2a-c>c-a,即c<$\frac{3}{2}$a,
由e=$\frac{c}{a}$,可得1<e<$\frac{3}{2}$.
故选:A.
点评 本题考查双曲线的离心率的范围,注意运用双曲线的定义和性质,考查化简整理的运算能力,属于中档题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
1.某空间几何体的三视图如图所示,则该几何体的体积为( )


| A. | 128 | B. | $\frac{128}{3}$ | C. | $\frac{64}{3}$ | D. | $\frac{32}{3}$ |
16.下列函数是偶函数,且在[0,1]上单调递增的是( )
| A. | y=sin(x+$\frac{π}{2}$) | B. | y=-cos4x | C. | y=-x2 | D. | y=|sin(π+x)| |
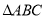 中,
中,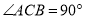 ,
,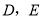 分别为
分别为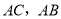 的中点,
的中点,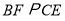 交
交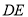 的延长线于点
的延长线于点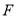 .
.
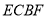 是平行四边形;
是平行四边形; 时,求证:四边形
时,求证:四边形