题目内容

2．若10件产品中有2件次品，现从中任取3件，则至少有一件是次品的取法共有（　　）
A．72种B．64种C．36种D．16种

分析 抽到的3件产品中至少有一件次品，1件次品，2件正品，和2件次品1件正品．

解答 解：抽到的3件产品中至少有一件次品的抽法有，C82C21+C81C22=64种．
故选：B．

点评 本题考查组合知识的运用，考查学生应用数学知识解决实际问题的能力，属于基础题．

练习册系列答案
相关题目
12．现有四个函数：①y=x•sinx；②y=x•cosx；③y=x•|cosx|；④y=x•2x的图象（部分）如图，则按照从左到右的顺序，图象对应的函数序号正确的一组是（　　）
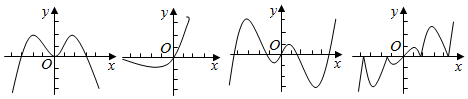
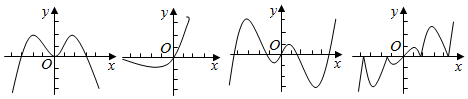
A．①④③②B．①④②③C．④①②③D．③④②①
13．若A（xl，y1），B（x2，y2）为平面上两点，则定义A?B=x1y1+x2y2，已知点M（$\sqrt{3}$，sinx），N（-1，cosx），设函数f（x）=M?N，将f（x）的图象向左平移φ（φ＞0）个单位长度后，所得图象关于y轴对称，则φ的最小值为（　　）
A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{5π}{6}$
10．下列各式中正确的是（　　）
A．sin（arcsin$\frac{π}{3}$）=$\frac{π}{3}$B．sin（arcsin$\frac{3}{π}$）=$\frac{3}{π}$
C．arccos（-x）=arccosxD．arctan（tan$\frac{2π}{3}$）=$\frac{2π}{3}$
17．从6名男生和4名女生中，选出3名男生和2名女生，分别担任五门不同课程的科代表．求不同分配方法的种数．
7．写出如图阴影部分的角的集合为{α|-150°+k•360°≤α≤150°+k•360°，k∈Z}．
14．已知f（x）=2sin（ωx+$\frac{π}{4}$），x∈R，其中ω是正实数，若函数f（x）图象上一个最高点与其相邻的一个最低点的距离为5，则ω的值是（　　）
A．$\frac{2π}{5}$B．$\frac{2π}{3}$C．$\frac{π}{5}$D．$\frac{π}{3}$
7．已知数列{an}是等差数列，数列{bn}是等比数列，公比为q，数列{cn}中，cn=anbn，Sn是数列{cn}前n项和，若Sm=11，S2m=7，S3m=-201（m为正偶数），则S4m的值为（　　）
A．-1601B．-1801C．-2001D．-2201
8．已知x，y是实数，则“$\left\{\begin{array}{l}{x＞1}\\{y＞1}\end{array}\right.$”是$\left\{\begin{array}{l}{x+y＞2}\\{xy＞1}\end{array}\right.$的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网