题目内容
已知(1-2x)6=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6,则a1+a2+a3+a4+a5+a6=( )
| A、-2 | B、-1 | C、0 | D、1 |
考点:二项式定理
专题:二项式定理
分析:在所给的等式中,令x=0求得a0 =1;再令x=1,可得要求的式子的值.
解答:
解:在(1-2x)6=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6 中,令x=0求得a0 =1.
再令x=1,可得a0+a1+a2+a3+a4+a5+a6=1,∴a1+a2+a3+a4+a5+a6=0,
故选:C.
再令x=1,可得a0+a1+a2+a3+a4+a5+a6=1,∴a1+a2+a3+a4+a5+a6=0,
故选:C.
点评:本题主要考查二项式定理的应用,是给变量赋值的问题,关键是根据要求的结果,选择合适的数值代入,属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
光线从点A(-3,5)射到x轴上,经反射以后经过点B(2,10),则光线从A到B的距离为( )
A、5
| ||
B、2
| ||
C、5
| ||
D、10
|
已知函数y=x2-2x+3在[0,a](a>0)上最大值是3,最小值是2,则实数a的范围是( )
| A、0<a<1 |
| B、0<a≤2 |
| C、1≤a≤2 |
| D、0≤a≤2 |
关于x的不等式(mx-1)(x-2)<0的解为2<x<
,则m的取值范围是( )
| 1 |
| m |
A、m<
| ||
| B、m>0 | ||
C、0<m<
| ||
| D、0<m<2 |
函数y=f(x)满足:
①y=f(x+1)是偶函数;
②在[1,+∞)上为增函数.
则f(-1)与f(2)的大小关系是( )
①y=f(x+1)是偶函数;
②在[1,+∞)上为增函数.
则f(-1)与f(2)的大小关系是( )
| A、f(-1)>f(2) |
| B、f(-1)<f(2) |
| C、f(-1)=f(2) |
| D、无法确定 |
若“0≤x≤4”是“(x-a)[x-(a+2)]≤0”的必要不充分条件,则实数a的取值范围是( )
| A、(0,2) |
| B、[0,2] |
| C、[-2,0] |
| D、(-2,0) |
设集合A={x|x2-x=0},B={x|x2+x=0},则集合A∪B=( )
| A、0 | B、{0} |
| C、∅ | D、{-1,0,1} |
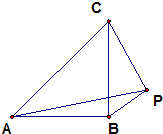 如图,在等腰直角△ABC中,∠ABC=90°,腰长为2,P为△ABC外一点,∠BPC=90°.
如图,在等腰直角△ABC中,∠ABC=90°,腰长为2,P为△ABC外一点,∠BPC=90°.