题目内容
12.若点A(-2,-3),B(-3,-2),直线l过点P(1,1)且与线段AB相交,则l的斜率k的取值范围是( )| A. | k≤-$\frac{4}{3}$或k≥-$\frac{3}{4}$ | B. | k≤$\frac{3}{4}$或k≥$\frac{4}{3}$ | C. | -$\frac{4}{3}$≤k≤-$\frac{3}{4}$ | D. | $\frac{3}{4}$≤k≤$\frac{4}{3}$ |
分析 由题意画出图形,求出P与线段两个端点连线的斜率得答案.
解答  解:如图,
解:如图,
∵${k}_{PA}=\frac{-3-1}{-2-1}=\frac{4}{3}$,${k}_{PB}=\frac{-2-1}{-3-1}=\frac{3}{4}$,
∴l的斜率k的取值范围是$\frac{3}{4}≤k≤\frac{4}{3}$.
故选:D.
点评 本题考查直线的斜率,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
2.直线a、b是异面直线,α、β是平面,若a?α,b?β,α∩β=c,则下列说法正确的是( )
| A. | c至少与a、b中的一条相交 | B. | c至多与a、b中的一条相交 | ||
| C. | c与a、b都相交 | D. | c与a、b都不相交 |
3.下列命题为真命题的是( )
| A. | 已知x,y∈R,则$\left\{\begin{array}{l}{x>1}\\{y>2}\end{array}\right.$是$\left\{\begin{array}{l}{x+y>3}\\{xy>2}\end{array}\right.$的充要条件 | |
| B. | 当0<x≤2时,函数y=x-$\frac{1}{x}$无最大值 | |
| C. | ?a,b∈R,$\frac{a+b}{2}≥\sqrt{ab}$ | |
| D. | ?x∈R,sinx+cosx=$\frac{7}{5}$ |
20.设f(x)=1-cosx,则f′($\frac{π}{2}$)等于( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
17.在△ABC中,角A、B、C的对边分别为a、b、c,a=3,A=45°,B=60°,则b=( )
| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{6}}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
4.“m>0”是“x2+x+m=0无实根”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
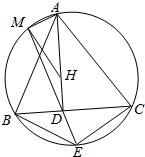 如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}$=$\frac{AB}{AC}$,直线ED交外接圆于点M,求证:∠AMH=90°.
如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}$=$\frac{AB}{AC}$,直线ED交外接圆于点M,求证:∠AMH=90°.