题目内容
设f(x)=lnx+ax(a∈R且a≠0).
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若a=1,证明:x∈[1,2]时,f(x)-3<
成立.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)若a=1,证明:x∈[1,2]时,f(x)-3<
| 1 |
| x |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)求函数的导数,即可讨论函数f(x)的单调性;
(Ⅱ)若a=1,构造函数,利用导数即可证明:x∈[1,2]时,f(x)-3<
成立.
(Ⅱ)若a=1,构造函数,利用导数即可证明:x∈[1,2]时,f(x)-3<
| 1 |
| x |
解答:
解:(Ⅰ)函数的定义域为(0,+∞),
函数的f(x)的导数f′(x)=
+a,
当a>0时,f′(x)>0,此时函数单调递增,
当a<0时,f′(x)=
+a=
,
由f′(x)>0,解得0<x<-
,
由f′(x)>0,解得x<-
,
∴函数f(x)在(0,-
)上增函数,则(-
,+∞)是减函数;
(Ⅱ)若a=1,f(x)=lnx+x,要证明:x∈[1,2]时,f(x)-3<
成立.
则只需要证明xlnx+x2-3x-1<0,
则g′(x)=lnx+2x-2,
∵g′(1)=0,
∴设h(x)=lnx+2x-2,h′(x)=
+2>0,x∈[1,2],
∴h(x)在x∈[1,2]上单调递增,∴g′(1)≤g′(x)≤g′(2),
即0≤g′(x)≤2+ln2,
∴g(x)在[1,2]上单调递增,∴g(x)≤g(2)=2ln2-3<0,
∴当x∈[1,2]时,xlnx+x2-3x-1<0恒成立,即原命题得证.
函数的f(x)的导数f′(x)=
| 1 |
| x |
当a>0时,f′(x)>0,此时函数单调递增,
当a<0时,f′(x)=
| 1 |
| x |
| ax+1 |
| x |
由f′(x)>0,解得0<x<-
| 1 |
| a |
由f′(x)>0,解得x<-
| 1 |
| a |
∴函数f(x)在(0,-
| 1 |
| a |
| 1 |
| a |
(Ⅱ)若a=1,f(x)=lnx+x,要证明:x∈[1,2]时,f(x)-3<
| 1 |
| x |
则只需要证明xlnx+x2-3x-1<0,
则g′(x)=lnx+2x-2,
∵g′(1)=0,
∴设h(x)=lnx+2x-2,h′(x)=
| 1 |
| x |
∴h(x)在x∈[1,2]上单调递增,∴g′(1)≤g′(x)≤g′(2),
即0≤g′(x)≤2+ln2,
∴g(x)在[1,2]上单调递增,∴g(x)≤g(2)=2ln2-3<0,
∴当x∈[1,2]时,xlnx+x2-3x-1<0恒成立,即原命题得证.
点评:本题主要考查函数的单调性和导数之间的关系,综合考查导数的应用.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
已知函数f(x)=
,设b>a≥0,若f(a)=f(b),则a•f(b)的取值范围是( )
|
A、[-
| ||||
B、[-
| ||||
C、[
| ||||
D、[
|
已知a+b>0,b<0,则( )
| A、a>b>-b>-a |
| B、a>-b>-a>b |
| C、a>b>-a>-b |
| D、a>-b>b>-a |
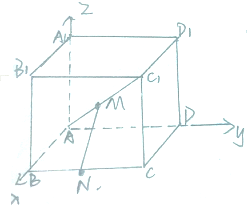 在棱长为1的正方体ABCD-A1B1C1D1中,动点M在线段AC1上,动点N在线段BC上,建立空间直角坐标系(如图所示),求线段MN长度最小值,以及此时点M,N的坐标.
在棱长为1的正方体ABCD-A1B1C1D1中,动点M在线段AC1上,动点N在线段BC上,建立空间直角坐标系(如图所示),求线段MN长度最小值,以及此时点M,N的坐标.