题目内容

计算定积分：
（1）
∫
0
-4
（
16-x2
+
2
1-2x
）dx=
 
；
（2）
∫
π
2
0
（sin2x+|（1-x）3|）dx=
 
．
考点：定积分
专题：导数的概念及应用
分析：（1）先根据定积分的几何意义求出：
∫
0
-4
16-x2
dx=4π，再根据定积分的法则求出
∫
0
-4
2
1-2x
dx，问题得以解决，
（2）先
∫
π
2
0
|（1-x）3|dx转化为
∫
1
0
（1-x）3dx+
∫
π
2
1
（x-1）3dx，然后计算即可．
解答： 解：（1）
∫
0
-4
16-x2
dx，表示以原点为圆心，以4为半径的圆的面积的四分之一，故：
∫
0
-4
16-x2
dx=
1
4
π×42=4π，
∫
0
-4
2
1-2x
dx=-ln（1-2x）|
 
0
-4
=-（ln1-ln9）=ln9，
∴
∫
0
-4
（
16-x2
+
2
1-2x
）dx=4π+ln9，
（2）
∫
π
2
0
sin2xdx=-
1
2
cos2x
|
π
2
0
=-
1
2
（cosπ-cos0）=1，
∫
π
2
0
|（1-x）3|dx=
∫
1
0
（1-x）3dx+
∫
π
2
1
（x-1）3dx=-
1
4
(1-x)4
|
1
0
+
1
4
（x-1）4|
 
π
2
1
=
1
4
+
1
4
(
π
2
-1)4，
故
∫
π
2
0
（sin2x+|（1-x）3|）dx=
5
4
+
1
4
(
π
2
-1)4，
故答案为：（1）=4π+ln9，（2）
5
4
+
1
4
(
π
2
-1)4，
点评：本题主要考查了定积分的计算，关键是转化的思想的利用，属于中档题．
练习册系列答案
相关题目
在（1+2x）4的展开式中，x3项的系数为
 
．
某商场对A品牌的商品进行了市场调查，预计2012年从1月起前x个月顾客对A品牌的商品的需求总量P（x）件与月份x的近似关系是：P（x）=
1
2
x（x+1）（41-2x）（x≤12且x∈N*）
（1）写出第x月的需求量f（x）的表达式；
（2）若第x月的销售量g（x）=
f(x)-21x，1≤x＜7且x∈N*
x2
ex
(
1
3
x2-10x+96)，7≤x≤12且x∈N*
（单位：件），每件利润q（x）元与月份x的近似关系为：q（x）=
10ex
x
，问：该商场销售A品牌商品，预计第几月的月利润达到最大值？月利润最大值是多少？（e6≈403）
已知定义在R上的函数y=f（x）满足下列三个条件：
①对于任意的x∈R，都有f（x+4）=f（x）；
②对于任意的0≤x1≤x2≤2，都有f（x1）＜f（x2）；
③函数y=f（x+2）是偶函数；
则下列结论中正确的是（　　）
A、f（6.5）＜f（5）＜f（15.5）
B、f（5）＜f（6.5）＜f（15.5）
C、f（5）＜f（15.5）＜f（6.5）
D、f（15.5）＜f（5）＜f（6.5）
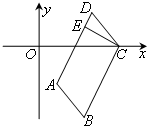如图，在平行四边形ABCD中，边AD所在直线方程为2x-y-2=0，顶点C（2，0）．
（Ⅰ）求边BC所在直线的方程；
（Ⅱ）求AD边上的高CE所在直线的方程．
函数y=cosx（sinx+
3
cosx）-
3
2
的图象（　　）
A、关于点（
π
3
，0）对称
B、关于直线x=
π
4
对称
C、关于点（
π
4
，0）对称
D、关于直线x=
π
3
对称
若?a∈（0，+∞），?θ∈R使asinθ≥a成立，则cos（θ-
π
6
）的值为（　　）
A、
3
2
B、
1
2
C、±
1
2
D、±
3
2
判断函数f（x）=x0-1的奇偶性：
 
．
已知复数
1+Z
1-Z
=i，则Z的虚部为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网