题目内容
12.在△ABC中,$\overrightarrow{AB}=(2,4)$,$\overrightarrow{AC}=(1,3)$,则$\overrightarrow{CB}$=( )| A. | (3,7) | B. | (3,5) | C. | (1,1) | D. | (1,-1) |
分析 根据向量的基本运算进行化简即可.
解答 解:$\overrightarrow{CB}$=$\overrightarrow{AB}$-$\overrightarrow{AC}$=(2,4)-(1,3)=(1,1),
故选:C
点评 本题主要考查向量的坐标运算,根据向量减法的法则是解决本题的关键.

练习册系列答案
相关题目
20.集合A={x|x2-4=0}的子集个数( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
17.已知tanα,$\frac{1}{tanα}$是关于x的方程x2-kx+k2-3=0的两个实根,且3π<α<$\frac{7}{2}$π,则cosα+sinα=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | -$\sqrt{3}$ |
4.在△ABC中,角A、B、C的对边分别为a,b,c,则“a=2bcosC”是“△ABC是等腰三角形”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
1.一个几何体的三视图如图所示,则该几何体的表面积为( )
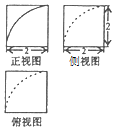

| A. | 24+π | B. | 24-3π | C. | 24-π | D. | 24-2π |