题目内容
已知函数f(x)=(1-
)9,则f′(x)中
的系数为( )
| 1 |
| x |
| 1 |
| x3 |
| A、-504 | B、-72 |
| C、72 | D、504 |
考点:导数的运算,二项式系数的性质
专题:高考数学专题,导数的概念及应用,二项式定理
分析:先求导,再根据二项定理,求得
的系数,问题得以解决.
| 1 |
| x |
解答:
解:∵f(x)=(1-
)9,
∴f′(x)=9(1-
)8•
,
∵f′(x)中
的系数就是f′(x)=9(1-
)8中
的系数,
∴T1=9
•(-
)=-72
,
则f′(x)中
的系数为-72,
故选:B.
| 1 |
| x |
∴f′(x)=9(1-
| 1 |
| x |
| 1 |
| x2 |
∵f′(x)中
| 1 |
| x3 |
| 1 |
| x |
| 1 |
| x |
∴T1=9
| C | 1 8 |
| 1 |
| x |
| 1 |
| x |
则f′(x)中
| 1 |
| x3 |
故选:B.
点评:本题主要考查了求导法则和二项式定理的展开式,属于基础题.

练习册系列答案
相关题目
函数f(x)=
+lg(10-x)的定义域为( )
| x2 | ||
|
| A、R |
| B、[1,10] |
| C、(-∞,-1)∪(1,10) |
| D、(1,10) |
已知函数f(x)的图象如图所示,则f(x)的解析式可以为( )
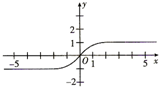

A、f(x)=x
| |||||||||
B、f(x)=
| |||||||||
C、f(x)=
| |||||||||
D、f(x)=
|
已知△ABC中,a=1,b=2,c=
,则∠C的大小为( )
| 7 |
| A、30° |
| B、120° |
| C、60°或80° |
| D、30°或150° |
已知A,B两地的距离为10km,B,C两地的距离为40km,现测得∠ABC=120°,则A,C两地的距离为( )
A、10
| ||
B、10
| ||
C、10
| ||
D、10
|
已知向量
=(-1,2),
=(5,k),若
∥
,则实数k的值为( )
| a |
| b |
| a |
| b |
| A、5 | B、-5 | C、10 | D、-10 |
已知数列an=3n-4,则29是该数列的( )
| A、第11项 | B、第13项 |
| C、第14项 | D、第15项 |
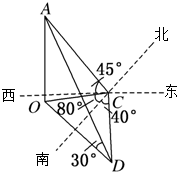 某人在C点测得某塔在南偏西80°的O处,塔顶A的仰角为45°,此人沿南偏东40°方向前进10米到D处,测得塔顶A的仰角为30°,求塔OA的高度?
某人在C点测得某塔在南偏西80°的O处,塔顶A的仰角为45°,此人沿南偏东40°方向前进10米到D处,测得塔顶A的仰角为30°,求塔OA的高度?