题目内容
设F（1，0），点M在x轴上，点P在y轴上，且
=2
，
⊥
．
（1）当点P在y轴上运动时，求点N的轨迹C的方程；
（2）设A（x1，y1），B（x2，y2），D（x3，y3）是曲线C上的点，且|
|，|
|，|
|成等差数列，当AD的垂直平分线与x轴交于点E（3，0）时，求B点坐标．
| MN |
| MP |
| PM |
| PF |
（1）当点P在y轴上运动时，求点N的轨迹C的方程；
（2）设A（x1，y1），B（x2，y2），D（x3，y3）是曲线C上的点，且|
| AF |
| BF |
| DF |
考点：轨迹方程,等差数列的通项公式
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）根据且
=2
，可得P为MN的中点，利用
⊥
，可得
•
=0，从而可得点N的轨迹C的方程；
（2）先根据抛物线的定义可知|
|=x1+
，|
|=x2+
，|
|=x3+
，利用|
|，|
|，|
|成等差数列，可得x1+x3=2x2，确定AD的中垂线方程，利用AD的中点在直线上，即可求得点B的坐标．
| MN |
| MP |
| PM |
| PF |
| PM |
| PF |
（2）先根据抛物线的定义可知|
| AF |
| p |
| 2 |
| BF |
| p |
| 2 |
| DF |
| p |
| 2 |
| AF |
| BF |
| DF |
解答：
解：（1）设N（x，y），则由
=2
，得P为MN的中点，
所以M（-x，0），P（0，
）
又
⊥
，∴
•
=0
∴y2=4x（x≠0）；
（2）由（1）知F（1，0）为曲线C的焦点，由抛物线定义知抛物线上任一点P0（x0，y0）到F的距离等于其到准线的距离，即|P0F|=x0+
故|
|=x1+
，|
|=x2+
，|
|=x3+
，
又|
|，|
|，|
|成等差数列
∴x1+x3=2x2，
∵直线AD的斜率kAD=
∴AD的中垂线方程为y=-
（x-3）
又AD的中点（
，
）在直线上，代入上式，得
=1，
∴x2=1
故所求点B的坐标为（1，±2）．
| MN |
| MP |
所以M（-x，0），P（0，
| y |
| 2 |
又
| PM |
| PF |
| PM |
| PF |
∴y2=4x（x≠0）；
（2）由（1）知F（1，0）为曲线C的焦点，由抛物线定义知抛物线上任一点P0（x0，y0）到F的距离等于其到准线的距离，即|P0F|=x0+
| p |
| 2 |
故|
| AF |
| p |
| 2 |
| BF |
| p |
| 2 |
| DF |
| p |
| 2 |
又|
| AF |
| BF |
| DF |
∴x1+x3=2x2，
∵直线AD的斜率kAD=
| 4 |
| y1+y3 |
∴AD的中垂线方程为y=-
| y1+y3 |
| 4 |
又AD的中点（
| x1+x3 |
| 2 |
| y1+y3 |
| 2 |
| x1+x3 |
| 2 |
∴x2=1
故所求点B的坐标为（1，±2）．
点评：本题考查求轨迹方程，考查向量知识的运用，考查数列知识，解题的关键是用好向量，挖掘隐含，属于中档题．
练习册系列答案
相关题目
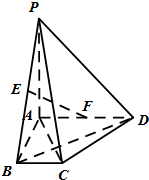如图，在四棱锥P-ABCD中，PA⊥面ABCD，AD∥BC，∠BAD=90°，AC⊥BD，BC=1，AD=PA=2，E，F分别为PB，AD的中点．