题目内容
14．若虚数z满足z3=27，则z3+z2+3z+3=21．分析 根据z3=27，利用立方差公式进行展开，利用整体代换进行求解即可．
解答 解：∵z3=27，
∴z3-27=0，
即（z-3）（z2+3z+9）=0，
∵z是虚数，因此z-3≠0，
则z2+3z+9=0，
则 z3+z2+3z+3=z3+（z2+3z+9）-6=27+0-6=21．
故答案为：21．
点评 本题主要考查复数的运算，利用立方差公式进行化简，利用整体代换是解决本题的关键．
练习册系列答案
相关题目
4．圆（x-3）2+（y+2）2=1与圆（x-7）2+（y-1）2=36的位置关系是（ ）
| A． | 外离 | B． | 外切 | C． | 相交 | D． | 内切 |
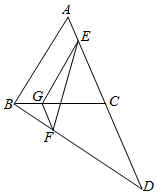如图，AB、CD是两条异面直线，AB=CD=3，E、F分别是AC、BD上的点，且AE：EC=BF：DF=1：2，EF=$\sqrt{7}$，求AB和CD所成角的大小．
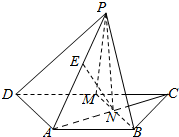如图．已知等腰梯形ABCD中，AB∥CD，AD=AB=$\frac{1}{2}$CD，M是的CD的中点．N是AC与BM的交点，将△BCM沿BM向上翻折成△BPM，使平面BPM⊥平面ABMD
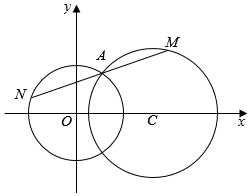如图，已知点A为圆O：x2+y2=9与圆C：（x-5）2+y2=16在第一象限内的交点．过A的直线1被圆O和圆C所截得的弦分别为NA，MA（M，N不重合）．若|NA|=|MA|，则直线1的方程是7x-24y+45=0．