题目内容
16.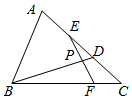 如图,在△ABC中,D、E分别是AB的两个三等分点,F在BC边上,且$\overrightarrow{BF}$=2$\overrightarrow{FC}$,EF与BD交于点P,则$\frac{|BP|}{|PD|}$=( )
如图,在△ABC中,D、E分别是AB的两个三等分点,F在BC边上,且$\overrightarrow{BF}$=2$\overrightarrow{FC}$,EF与BD交于点P,则$\frac{|BP|}{|PD|}$=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 设$\frac{|BP|}{|PD|}$=x,$\frac{|FP|}{|EP|}$=y,$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,从而可得($\frac{1}{3}$•$\frac{x}{1+x}$-$\frac{y}{1+y}$•$\frac{2}{3}$)$\overrightarrow{a}$+($\frac{2}{3}$•$\frac{x}{1+x}$+$\frac{y}{1+y}$•$\frac{1}{3}$)$\overrightarrow{b}$=$\frac{2}{3}$$\overrightarrow{b}$,从而可得$\frac{1}{3}$•$\frac{x}{1+x}$-$\frac{y}{1+y}$•$\frac{2}{3}$=0且$\frac{2}{3}$•$\frac{x}{1+x}$+$\frac{y}{1+y}$•$\frac{1}{3}$=$\frac{2}{3}$,从而解得.
解答 解:设$\frac{|BP|}{|PD|}$=x,$\frac{|FP|}{|EP|}$=y,$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,
则$\overrightarrow{BD}$=$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{CA}$=$\overrightarrow{b}$+$\frac{1}{3}$($\overrightarrow{a}$-$\overrightarrow{b}$)=$\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$;
故$\overrightarrow{BP}$=$\frac{x}{1+x}$$\overrightarrow{BD}$=$\frac{x}{1+x}$($\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$),
$\overrightarrow{FE}$=$\frac{1}{3}$$\overrightarrow{b}$+$\frac{2}{3}$($\overrightarrow{a}$-$\overrightarrow{b}$)=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$,
故$\overrightarrow{FP}$=$\frac{y}{1+y}$($\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$),
$\overrightarrow{BP}$-$\overrightarrow{FP}$=$\frac{x}{1+x}$($\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$)-$\frac{y}{1+y}$($\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$)=$\overrightarrow{BF}$=$\frac{2}{3}$$\overrightarrow{b}$,
∴($\frac{1}{3}$•$\frac{x}{1+x}$-$\frac{y}{1+y}$•$\frac{2}{3}$)$\overrightarrow{a}$+($\frac{2}{3}$•$\frac{x}{1+x}$+$\frac{y}{1+y}$•$\frac{1}{3}$)$\overrightarrow{b}$=$\frac{2}{3}$$\overrightarrow{b}$,
∴$\frac{1}{3}$•$\frac{x}{1+x}$-$\frac{y}{1+y}$•$\frac{2}{3}$=0且$\frac{2}{3}$•$\frac{x}{1+x}$+$\frac{y}{1+y}$•$\frac{1}{3}$=$\frac{2}{3}$,
∴$\frac{x}{1+x}$=$\frac{4}{5}$,
故x=4;
故选:C.
点评 本题考查了平面向量的线性运算的应用及数形结合的思想应用.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案| A. | $\root{6}{{{{(-3)}^2}}}=\root{3}{-3}$ | B. | $\root{4}{a^4}=a$ | C. | $\root{6}{2^2}=\root{3}{2}$ | D. | a0=1 |
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{1}{{\sqrt{3}}}$ | D. | -$\frac{1}{{\sqrt{3}}}$ |
| A. | {锐角} | B. | {小于90°的角} | ||
| C. | {第一象限角} | D. | {α|k•360°<α<k•360°+90°(k∈Z,k≤0)} |