题目内容
1.已知sin($\frac{π}{4}$-α)=$\frac{1}{3}$,0<α<$\frac{π}{4}$,则$\frac{cos(2π-2α)}{cos(\frac{5π}{4}+α)}$=-$\frac{2\sqrt{2}}{3}$.分析 由条件利用同角三角的基本关系求出cos($\frac{π}{4}$-α) 的值,利用三角恒等变换把要求的式子化简为-cos($\frac{π}{4}$-α),可得结论.
解答 解:∵sin($\frac{π}{4}$-α)=$\frac{1}{3}$,0<α<$\frac{π}{4}$,∴cos($\frac{π}{4}$-α)=$\sqrt{{1-sin}^{2}(\frac{π}{4}-α)}$=$\frac{2\sqrt{2}}{3}$.
则$\frac{cos(2π-2α)}{cos(\frac{5π}{4}+α)}$=$\frac{cos2α}{-cos(\frac{π}{4}+α)}$=$\frac{sin(\frac{π}{2}+2α)}{-cos(\frac{π}{4}+α)}$=$\frac{2sin(\frac{π}{4}+α)cos(\frac{π}{4}+α)}{-cos(\frac{π}{4}+α)}$=-2sin($\frac{π}{4}$+α)
=-cos[$\frac{π}{2}$-($\frac{π}{4}$+α)]=-cos($\frac{π}{4}$-α)=-$\frac{2\sqrt{2}}{3}$,
故答案为:-$\frac{2\sqrt{2}}{3}$.
点评 本题主要考查同角三角的基本关系,三角恒等变换,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.函数y=3x+$\frac{12}{{x}^{2}}$(x>0)的最小值是( )
| A. | 6 | B. | 6$\sqrt{6}$ | C. | 9 | D. | 12 |
6.若a=${∫}_{-1}^{1}$$\sqrt{1-{x}^{2}}$dx,则($\frac{a}{π}x-\frac{1}{x}$)6的展开式中的常数项与x最低次幂项的系数比为( )
| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
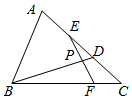 如图,在△ABC中,D、E分别是AB的两个三等分点,F在BC边上,且$\overrightarrow{BF}$=2$\overrightarrow{FC}$,EF与BD交于点P,则$\frac{|BP|}{|PD|}$=( )
如图,在△ABC中,D、E分别是AB的两个三等分点,F在BC边上,且$\overrightarrow{BF}$=2$\overrightarrow{FC}$,EF与BD交于点P,则$\frac{|BP|}{|PD|}$=( )