题目内容
8.已知函数$f(x)=1+x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+…+\frac{{{x^{2013}}}}{2013}$,$g(x)=1-x+\frac{x^2}{2}-\frac{x^3}{3}+\frac{x^4}{4}+…$$-\frac{{{x^{2013}}}}{2013}$,设函数F(x)=f(x+1)•g(x-1),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b-a的最小值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 求导数,确定f(x)是R上的增函数,函数f(x)在[-1,0]上有一个零点,同理可得函数g(x)在[0,1]上有一个零点;再由图象平移和函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,求出a的最大值和b的最小值,即可得出结论.
解答 解:f′(x)=1-x+x2-x3+…+x2012;
x>-1时,f′(x)=$\frac{1-(-x)^{2013}}{1-(-x)}$>0,f′(-1)=2013>0,x<-1时,f′(x)>0,
因此f(x)是R上的增函数,
∵f(0)=1>0,f(-1)=(1-1)+(-$\frac{1}{2}$-$\frac{1}{3}$)+…+(-$\frac{1}{2012}$-$\frac{1}{2013}$)<0
∴函数f(x)在[-1,0]上有一个零点;
∴函数f(x+1)在[-2,-1]上有一个零点,
同理,g′(x)=-1+x-x2+…-x2012;
x>-1时,g′(x)=-$\frac{1+{x}^{2013}}{1+x}$<0,g′(-1)=-2013<0,x<-1时,g′(x)<0,
因此g(x)是R上的减函数,
∵g(0)=-1<0,g(1)=(1-1)+($\frac{1}{2}$-$\frac{1}{3}$)+…+($\frac{1}{2012}$-$\frac{1}{2013}$)>0,
∴函数g(x)在[0,1]上有一个零点;
∴函数g(x-1)在[1,2]上有一个零点,
∵函数F(x)=f(x+1)•g(x-1)的零点均在区间[a,b],(a,b∈Z)内,
∴amax=-2,bmin=2,
∴(b-a)min=2-(-2)=4.
故选:B.
点评 此题是难题.考查函数零点判定定理和利用导数研究函数的单调性以及数列求和问题以及函数图象的平移,学生灵活应用知识分析解决问题的能力.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\frac{\sqrt{3}}{3}$ |
”发生的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2-\sqrt{2}}{2}$ | C. | $\frac{3-\sqrt{3}}{3}$ | D. | $\frac{2-\sqrt{3}}{2}$ |
| A. | -$\frac{\sqrt{3}}{5}$ | B. | $\frac{3\sqrt{3}}{5}$ | C. | $\frac{\sqrt{3}}{7}$ | D. | $\frac{\sqrt{3}}{19}$ |
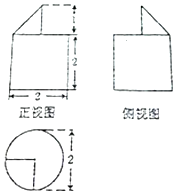
| A. | 6π+1 | B. | $\frac{{({24+\sqrt{2}})π}}{4}+1$ | C. | $\frac{{({23+\sqrt{2}})π}}{4}+\frac{1}{2}$ | D. | $\frac{{({23+\sqrt{2}})π}}{4}+1$ |
| A. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$+2$\overrightarrow{b}$=0 | C. | $\frac{\overrightarrow{a}}{|\overrightarrow{a}|}$+$\frac{\overrightarrow{b}}{|\overrightarrow{b}|}$=0 | D. | 2$\overrightarrow{a}$+$\overrightarrow{b}$=0 |
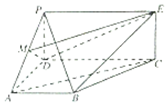 如图所示的几何体中,四边形PDCE为矩形,ABCD为直角梯形,且∠BAD=∠ADC=90°,平面PDCE⊥平面ABCD,AB=AD=$\frac{1}{2}$CD=1,PD=$\sqrt{2}$.
如图所示的几何体中,四边形PDCE为矩形,ABCD为直角梯形,且∠BAD=∠ADC=90°,平面PDCE⊥平面ABCD,AB=AD=$\frac{1}{2}$CD=1,PD=$\sqrt{2}$.