题目内容
3.若tanα=4sin420°,则tan(α-60°)的值为( )| A. | -$\frac{\sqrt{3}}{5}$ | B. | $\frac{3\sqrt{3}}{5}$ | C. | $\frac{\sqrt{3}}{7}$ | D. | $\frac{\sqrt{3}}{19}$ |
分析 根据tanα=4sin420°,求解出tanα的值,将tan(α-60°)利用正切的和与差公式展开,即可得解.
解答 解:由题意tanα=4sin420°,可得:tanα=4sin60°=2$\sqrt{3}$.
由tan(α-60°)=$\frac{tanα-tan60°}{1+tan•tanα60°}$=$\frac{2\sqrt{3}-\sqrt{3}}{1+2\sqrt{3}×\sqrt{3}}$=$\frac{\sqrt{3}}{7}$.
故选C.
点评 本题主要考查了正切的和与差公式和诱导公式的化简能力.属于基础题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
18.若tan(α+80°)=4sin420°,则tan(α+20°)的值为( )
| A. | -$\frac{\sqrt{3}}{5}$ | B. | $\frac{3\sqrt{3}}{5}$ | C. | $\frac{\sqrt{3}}{19}$ | D. | $\frac{\sqrt{3}}{7}$ |
13.拖延症总是表现在各种小事上,但日积月累,特别影响个人发展,某校的一个社会实践调查小组,在对该校学生进行“是否有明显拖延症”的调查中,随机发放了110份问卷.对收回的100份有效问卷进行统计,得到如下2×2列联表:
(Ⅰ)按女生是否有明显拖延症进行分层,已经从40份女生问卷中抽取了8份问卷,现从这8份问卷中再随机抽取3份,并记其中无明显拖延症的问卷的份数为X,试求随机变量X的分布列和数学期望;
(2)若在犯错误的概率不超过P的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的P的值应为多少?请说明理由
附:独立性检验统计量K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d
| 有明显拖延症 | 无明显拖延症 | 合计 | |
| 男 | 35 | 25 | 60 |
| 女 | 30 | 10 | 40 |
| 总计 | 65 | 35 | 100 |
(2)若在犯错误的概率不超过P的前提下认为无明显拖延症与性别有关,那么根据临界值表,最精确的P的值应为多少?请说明理由
附:独立性检验统计量K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
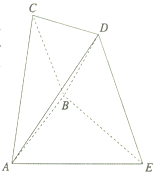 在如图所示的空间几何体中,边长为2的正三角形ABC所在平面与正三角形ABE所在平面互相垂直,DE在平面ABE内的射影为∠AEB的平分线且DE与平面AEB所成的角为60°,DE=2.
在如图所示的空间几何体中,边长为2的正三角形ABC所在平面与正三角形ABE所在平面互相垂直,DE在平面ABE内的射影为∠AEB的平分线且DE与平面AEB所成的角为60°,DE=2.