题目内容
3．
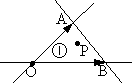如图，已知O，A，B是平面内不共线的三点，且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$，直线OA，OB，AB将平面区域分成7部分，若点P落在区域①中（含边界），则z=2x+y的最大值为（ ）| A． | 不存在 | B． | 0 | C． | 1 | D． | 2 |
分析 由题意，点P在△OAB内（含边界）运动，且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$，得到x，y的约束条件，求目标函数的最大值即可．
解答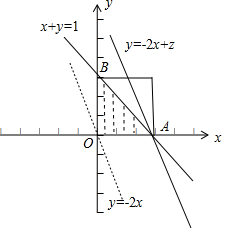 
解：因为点P在△OAB内（含边界）运动，且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$，
所以$\left\{\begin{array}{l}{0≤x≤1}\\{0≤y≤1}\\{x+y≤1}\end{array}\right.$，
画出不等式组对应的平面区域，如图所示，
由z=2x+y，
当直线y=-2x+z经过点A（1，0）时，在y轴的截距最大，
所以z的最大值为2．
故选：D．
点评 本题考查了平面向量基本定理以及简单的线性规划问题，是综合性题目．
练习册系列答案
相关题目
18．已知a，b为正实数，a+b=1，且a，b的值使$\frac{1}{a}+\frac{4}{b}$取得最小值，此最小值为m，则函数f（x）=ax3-4x2-mx+1的极大值为（ ）
| A． | 4 | B． | $\frac{25}{3}$ | C． | -89 | D． | $\frac{17}{3}$ |
8．已知椭圆的中心在原点，离心率e=$\frac{1}{2}$，且它的一个焦点与抛物线x2=-4y的焦点重合，则此椭圆的方程为（ ）
| A． | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$ | B． | $\frac{{x}^{2}}{3}+\frac{{y}^{2}}{4}=1$ | C． | ${x}^{2}+\frac{{y}^{2}}{2}=1$ | D． | $\frac{{x}^{2}}{6}+\frac{{y}^{2}}{8}=1$ |
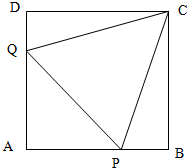如图，正方形ABCD的边长为1，P，Q分别为边AB，DA上的点，且都不与A，B，D重合，线段PQ的长为1，△CPQ的面积用y表示．