题目内容
设函数f(x)=
ax3+
bx2+(1-2a)x,a,b∈R,a≠0.
(1)若b=4a,求f(x)的单调递增区间;
(2)若曲线y=f(x)与x轴相切于异于原点的一点,且f(x)的极小值为-
a,求a,b的值.
| 1 |
| 3 |
| 1 |
| 2 |
(1)若b=4a,求f(x)的单调递增区间;
(2)若曲线y=f(x)与x轴相切于异于原点的一点,且f(x)的极小值为-
| 4 |
| 3 |
考点:利用导数研究函数的极值
专题:综合题,导数的综合应用
分析:(1)求导数,分类讨论,利用导数的正负,即可求f(x)的单调递增区间;
(2)依据题意得:依据题意得:
=
≠0,得到a,b之间的关系式,再根据极小值,则求导求出极小值点,得到关于a,b的另外一个等式,即可求出a,b的值.
(2)依据题意得:依据题意得:
| 9b2 |
| 16a2 |
| 3-6a |
| a |
解答:
 解:(1)∵f(x)=
解:(1)∵f(x)=
ax3+
bx2+(1-2a)x,
∴f′(x)=ax2+4ax2+(1-2a).
令f′(x)=0,△=4a(6a-1)
当a<0或a>
时,由f′(x)=0得x=-2±
.
①当a<0时,f(x)的单调递增区间为(-2+
,-2-
);…(3分)
②当0<a≤
时,f(x)的单调递增区间为R;…(5分)
③当a>
时,f(x)的单调递增区间为(-∞,-2-
),(-2+
,+∞)…(7分)
(2)依据题意得:
=
≠0,
f′(x)=a(x+
)(x+
)=0,得x=-
或x=-
.
如图,得f(-
)=-
a,
∴
(-
)(-
+
)2=-
a,则b=4a,
代入
=
得,b=
,a=
.…(15分)
 解:(1)∵f(x)=
解:(1)∵f(x)=| 1 |
| 3 |
| 1 |
| 2 |
∴f′(x)=ax2+4ax2+(1-2a).
令f′(x)=0,△=4a(6a-1)
当a<0或a>
| 1 |
| 6 |
| ||
| a |
①当a<0时,f(x)的单调递增区间为(-2+
| ||
| a |
| ||
| a |
②当0<a≤
| 1 |
| 6 |
③当a>
| 1 |
| 6 |
| ||
| a |
| ||
| a |
(2)依据题意得:
| 9b2 |
| 16a2 |
| 3-6a |
| a |
f′(x)=a(x+
| 3b |
| 4a |
| b |
| 4a |
| 3b |
| 4a |
| b |
| 4a |
如图,得f(-
| b |
| 4a |
| 4 |
| 3 |
∴
| a |
| 3 |
| b |
| 4a |
| b |
| 4a |
| 3b |
| 4a |
| 4 |
| 3 |
代入
| 9b2 |
| 16a2 |
| 3-6a |
| a |
| 4 |
| 5 |
| 1 |
| 5 |
点评:本题以函数为载体,考查含参二次不等式,考查导数知识的运用,考查曲线的切线,同时考查零点存在性定理,综合性比较强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
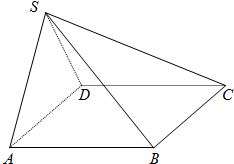 如图,在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,侧面SAD为正三角形,且垂直于底面ABCD.
如图,在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,侧面SAD为正三角形,且垂直于底面ABCD. 已知正三棱柱ABC-A1B1C1中,AB=2,AA1=
已知正三棱柱ABC-A1B1C1中,AB=2,AA1= 如图,正方形ABCD所在平面与正方形ABEF所在平面构成45°的二面角,则异面直线
如图,正方形ABCD所在平面与正方形ABEF所在平面构成45°的二面角,则异面直线