题目内容
11.已知函数f(x)=|x-2|+|2x+1|.(Ⅰ)解不等式f(x)>5;
(Ⅱ)若关于x的方程$\frac{1}{f(x)-4}$=a的解集为空集,求实数a的取值范围.
分析 (Ⅰ)分类讨论求得原不等式解集.
(Ⅱ)由分段函数f(x)的解析式可得f(x)的单调性,由此求得函数f(x)的值域,求出$\frac{1}{f(x)-4}$的取值范围.再根据关于x的方程$\frac{1}{f(x)-4}$=a的解集为空集,求得实数a的取值范围.
解答 解:(Ⅰ)解不等式|x-2|+|2x+1|>5,
x≥2时,x-2+2x+1>5,解得:x>2;
-$\frac{1}{2}$<x<2时,2-x+2x+1>5,无解,
x≤-$\frac{1}{2}$时,2-x-2x-1>5,解得:x<-$\frac{4}{3}$,
故不等式的解集是(-∞,-$\frac{4}{3}$)∪(2,+∞);
(Ⅱ)f(x)=|x-2|+|2x+1|=$\left\{\begin{array}{l}{3x+1,x≥2}\\{x+3,-\frac{1}{2}<x<2}\\{-3x+1,x≤-\frac{1}{2}}\end{array}\right.$,
故f(x)的最小值是$\frac{5}{2}$,所以函数f(x)的值域为[$\frac{5}{2}$,+∞),
从而f(x)-4的取值范围是[-$\frac{3}{2}$,+∞),
进而$\frac{1}{f(x)-4}$的取值范围是(-∞,-$\frac{2}{3}$]∪(0,+∞).
根据已知关于x的方程$\frac{1}{f(x)-4}$=a的解集为空集,所以实数a的取值范围是(-$\frac{2}{3}$,0].
点评 本题主要考查带有绝对值的函数,绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
1.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,且|$\overrightarrow{a}$|=2$\sqrt{3}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{6}$,$\overrightarrow{a}$⊥(3$\overrightarrow{a}$-$\overrightarrow{b}$),则|$\overrightarrow{b}$|等于( )
| A. | 6 | B. | 6$\sqrt{3}$ | C. | 12 | D. | 12$\sqrt{3}$ |
2.已知双曲线M的实轴长为2,且它的一条渐近线方程为y=2x,则双曲线M的标准方程可能是( )
| A. | x2-4y2=1 | B. | $\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{64}$=1 | C. | $\frac{{y}^{2}}{4}$-x2=1 | D. | y2-4x2=1 |
16.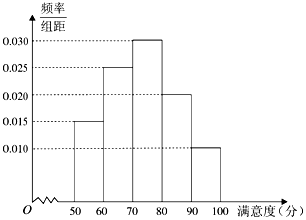 某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:
某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:
(Ⅰ)根据A公司的频率分布直方图,估计该公司满意度评分的中位数;
(Ⅱ)从满意度高于90分的问卷中随机抽取两份,求这两份问卷都是给A公司评分的概率;
(Ⅲ)请从统计角度,对A、B两家公司做出评价.
 某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:
某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:| 满意度 评分分组 | 频数 |
| [50,60) | 2 |
| [60,70) | 8 |
| [70,80) | 14 |
| [80,90) | 14 |
| [90,100] | 2 |
(Ⅱ)从满意度高于90分的问卷中随机抽取两份,求这两份问卷都是给A公司评分的概率;
(Ⅲ)请从统计角度,对A、B两家公司做出评价.