题目内容
20.函数g(x)=ax3+2(1-a)x2-3ax在区间(-∞,$\frac{a}{3}$)内单调递减,则a的取值范围为( )| A. | a≥1 | B. | a≤1 | C. | a≥-1 | D. | -1≤a≤0 |
分析 由g′(x)=3ax2+4(1-a)x-3a,g(x)在(-∞,$\frac{a}{3}$)递减,则g′(x)在(-∞,$\frac{a}{3}$)上小于等于0,讨论(1)a=0时,(2)a>0,(3)a<0时的情况,从而求出a的范围.
解答 解:∵g′(x)=3ax2+4(1-a)x-3a,g(x)在(-∞,$\frac{a}{3}$)递减,
则g′(x)在(-∞,$\frac{a}{3}$)上小于等于0,即:3ax2+4(1-a)x-3a≤0,
(1)a=0时,g′(x)≤0,解得:x≤0,即g(x)的减区间是(-∞,0),
∴$\frac{a}{3}$≤0,才能g(x)在(-∞,$\frac{a}{3}$)递减,解得a=0 成立.
(2)a>0,g′(x)是一个开口向上的抛物线,
要使g′(x)在(-∞,$\frac{a}{3}$)上小于等于0 解得:a无解;
(3)a<0,g′(x)是一个开口向下的抛物线,
设g′(x)与x轴的左右两交点为A(x1,0),B(x2,0)
由韦达定理,知x1+x2=-$\frac{4(1-a)}{3a}$,x1x2=-1,
解得:x1=-$\frac{2(1-a)+\sqrt{13{a}^{2}-8a+4}}{3a}$,
则在A左边和B右边的部分g′(x)≤0 又知g(x)在(-∞,$\frac{a}{3}$)递减,
即g′(x)在(-∞,$\frac{a}{3}$)上小于等于0,
∴x1≥$\frac{a}{3}$,即:解得-1≤a≤5,取交集,得-1≤a<0,
∴a的取值范围是-1≤a≤0.
故选:D.
点评 本题考察了函数的单调性,导数的应用,渗透了分类讨论思想,是一道综合题.

练习册系列答案
相关题目
8.已知集合A={-$\frac{1}{3}$,$\frac{1}{2}$},B={x|ax+1=0}},且B⊆A,则a的可取值组成的集合为( )
| A. | {-3,2} | B. | {-3,0,2} | C. | {3,-2} | D. | {3,0,-2} |
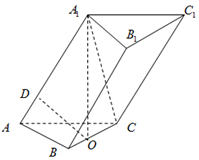 三棱柱ABC-A1B1C1的底面ABC是等边三角形,BC的中点为O,A1O⊥底面ABC,AA1与底面ABC所成的角为$\frac{π}{3}$,点D在棱AA1上,且AD=$\sqrt{3}$,AB=4.
三棱柱ABC-A1B1C1的底面ABC是等边三角形,BC的中点为O,A1O⊥底面ABC,AA1与底面ABC所成的角为$\frac{π}{3}$,点D在棱AA1上,且AD=$\sqrt{3}$,AB=4. 如图所示,单位位圆上的两个向量$\overrightarrow{a},\overrightarrow{b}$相互垂直,若向量$\overrightarrow{c}$满足($\overrightarrow{c}-\overrightarrow{a}$)•($\overrightarrow{c}-\overrightarrow{b}$)=0,则|$\overrightarrow{c}$|的取值范围是( )
如图所示,单位位圆上的两个向量$\overrightarrow{a},\overrightarrow{b}$相互垂直,若向量$\overrightarrow{c}$满足($\overrightarrow{c}-\overrightarrow{a}$)•($\overrightarrow{c}-\overrightarrow{b}$)=0,则|$\overrightarrow{c}$|的取值范围是( )