题目内容
4.幂函数f(x)=(m2-m-1)x-m在x∈(0,+∞)时为减函数,则m的值为2.分析 利用幂函数的定义和单调性即可求出.
解答 解:∵幂函数y=(m2-m-1)x-m在x∈(0,+∞)时为减函数,
∴m必满足 $\left\{\begin{array}{l}{{m}^{2}-m-1=1}\\{-m<0}\end{array}\right.$,解得m=2,即y=x-2.
故答案为:2.
点评 熟练掌握幂函数的定义和单调性是解题的关键.

练习册系列答案
相关题目
12.已知$\overrightarrow{OA}=(1,1,0)$,$\overrightarrow{OB}=(4,1,0)$,$\overrightarrow{OC}=(4,5,-1)$,则向量$\overrightarrow{AB}$和$\overrightarrow{AC}$的夹角的余弦值为( )
| A. | $\frac{{\sqrt{26}}}{26}$ | B. | $\frac{{\sqrt{26}}}{12}$ | C. | $\frac{{3\sqrt{26}}}{26}$ | D. | $\frac{{2\sqrt{26}}}{13}$ |
9.已知θ是第一象限角,且$cosθ=\frac{{\sqrt{10}}}{10}$,则$\frac{cos2θ}{{sin2θ+co{s^2}θ}}$的值是( )
| A. | $\frac{8}{7}$ | B. | $-\frac{8}{7}$ | C. | $\frac{10}{7}$ | D. | $-\frac{10}{7}$ |
16.定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0)(x1≠x2),有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<0,则( )
| A. | f(-3)<f(-2)<f(1) | B. | f(1)<f(-2)<f(-3) | C. | f(-2)<f(1)<f(-3) | D. | f(-3)<f(1)<f(-2) |
14.已知函数f(x)=|xex|-t有三个零点,则实数t的取值范围为( )
| A. | (0,$\frac{1}{e}$) | B. | (0,1) | C. | ($\frac{1}{e}$,1) | D. | (0,$\frac{1}{e}$] |
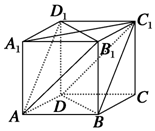 在正方体ABCD-A1B1C1D1中,如图.
在正方体ABCD-A1B1C1D1中,如图.