题目内容
3.如图在边长为4的正方形铁皮的四角切去相等的正方形,在把它的边沿虚线折起,做成一个无盖的方底盒子.问:切去的小正方形边长为多少时,盒子容积最大?最大容积V1是多少?
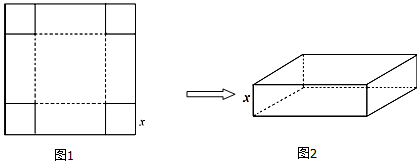
分析 由已知得长方体容积V1=(4-2x)2•x=4(x3-4x2+4x),(0<x<2),求导数,确定函数的单调性,即可得出结论.
解答 解:设切去的正方形边长为x,则焊接成的盒子的底面边长为4-2x,高为x.
所以V1=(4-2x)2•x=4(x3-4x2+4x),(0<x<2)
∴V1′=4(3x2-8x+4).
令V1′=0得x1=$\frac{2}{3}$,x2=2(舍去),
当x<$\frac{2}{3}$时,V1′>0,当$\frac{2}{3}$<x<2时,V1′<0,
∴当x=$\frac{2}{3}$时盒子容积最大,最大容积V1是$\frac{128}{27}$.
点评 本题重点考查利用导数研究函数的性质,利用函数的性质解决不等式、方程问题.重点考查学生的代数推理论证能力.

练习册系列答案
相关题目
14.若中心在原点,焦点在y轴上的双曲线离心率为$\sqrt{3}$,则此双曲线的渐近线方程为( )
| A. | y=±x | B. | $y=±\frac{{\sqrt{2}}}{2}x$ | C. | $y=±\sqrt{2}x$ | D. | $y=±\frac{1}{2}x$ |
12.已知$\overrightarrow a=({1,cosa}),\overrightarrow b=({sina,1})$,若$\overrightarrow a⊥\overrightarrow b$,则sin2α=( )
| A. | $-\frac{1}{2}$ | B. | -1 | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
19.设F为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的右焦点,若OF的垂直平分线与渐近线在第一象限内的交点到另一条渐近线的距离为$\frac{1}{2}|OF|$,则双曲线的离心率为( )
| A. | $2\sqrt{2}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $2\sqrt{3}$ | D. | 3 |
12.已知$\overrightarrow{OA}=(1,1,0)$,$\overrightarrow{OB}=(4,1,0)$,$\overrightarrow{OC}=(4,5,-1)$,则向量$\overrightarrow{AB}$和$\overrightarrow{AC}$的夹角的余弦值为( )
| A. | $\frac{{\sqrt{26}}}{26}$ | B. | $\frac{{\sqrt{26}}}{12}$ | C. | $\frac{{3\sqrt{26}}}{26}$ | D. | $\frac{{2\sqrt{26}}}{13}$ |
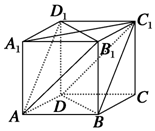 在正方体ABCD-A1B1C1D1中,如图.
在正方体ABCD-A1B1C1D1中,如图.