题目内容
17.若函数f(2x+1)=x2-2x+1,则f(3)=0.分析 令2x+1=t,则x=$\frac{t-1}{2}$则f(t)=${(\frac{t-1}{2}-1)}^{2}$,令t=3,求出f(3)的值即可.
解答 解:函数f(2x+1)=x2-2x+1=(x-1)2,
令2x+1=t,则x=$\frac{t-1}{2}$
则f(t)=${(\frac{t-1}{2}-1)}^{2}$,
故f(3)=${(\frac{3-1}{2}-1)}^{2}$=0,
故答案为:0.
点评 本题考查了函数求值问题,考查求函数的解析式问题,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.数列 {an}满足 an+1=$\frac{1}{1-{a}_{n}}$,a1=2,则a2016的值是( )
| A. | 2 | B. | -1 | C. | 0 | D. | $\frac{1}{2}$ |
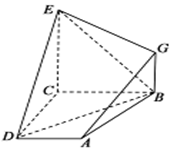 如图,已知四边形BCD和BCEG均为直角梯形,AD∥EG、CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=2AD,CE=2BG.求证:
如图,已知四边形BCD和BCEG均为直角梯形,AD∥EG、CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=2AD,CE=2BG.求证: