题目内容
20.已知圆的方程为(x-1)2+(y-1)2=1,P点坐标为(2,3),求:(1)过P点的圆的切线长.
(2)过P点的圆的切线方程.
分析 (1)利用勾股定理,求出过P点的圆的切线长.
(2)分类讨论,利用圆心到直线的距离等于半径,即可过P点的圆的切线方程.
解答 解:(1)圆的圆心C为(1,1),CA=CB=1,|PC|=$\sqrt{(2-1)^{2}+(3-1)^{2}}$=$\sqrt{5}$,则切线长|PA|=$\sqrt{5-1}$=2,…(4分)
(2)若切线的斜率存在,可设切线的方程为y-3=k(x-2)
即kx-y-2k+3=0
则圆心到切线的距离$d=\frac{|k-1-2k+3|}{{\sqrt{{k^2}+1}}}=1$,解得$k=\frac{3}{4}$
故切线的方程为3x-4y+6=0…(8分)
若切线的斜率不存在,切线方程为x=2,此时直线也与圆相切.…(11分)
综上所述,过P点的切线的方程为3x-4y+6=0和x=2.…(12分)
点评 本题考查直线与圆的位置关系,考查勾股定理的运用,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
13.集合$A=\left\{{x|f(x)=\sqrt{{2^x}-1}}\right\}$,$B=\left\{{y|y={{log}_2}({{2^x}+2})}\right\}$,则A∩∁RB=( )
| A. | (1,+∞) | B. | [0,1] | C. | [0,1) | D. | [0,2) |
11.已知四边形ABCD为正方形,点E是CD的中点,若$\overrightarrow{AB}$=$\vec a$,$\overrightarrow{AD}$=$\vec b$,则$\overrightarrow{BE}$=( )
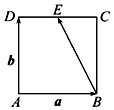

| A. | $\frac{1}{2}$$\vec b$+$\vec a$ | B. | $\vec b$$-\frac{1}{2}$$\vec a$ | C. | $\frac{1}{2}$$\vec a$+$\vec b$ | D. | $\vec a$-$\frac{1}{2}$$\vec b$ |
12.若集合M={y|y=$\frac{1}{{x}^{2}}$},N={x|y=$\sqrt{x-1}$},那么M∩N=( )
| A. | (0,+∞) | B. | (1,+∞) | C. | [1,+∞) | D. | [0,+∞) |
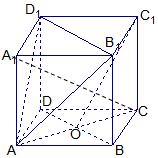 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.求证:
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.求证: