题目内容
6.已知O是坐标原点,实数x,y满足$\left\{\begin{array}{l}{2x-y-1≤0}\\{x+y-3≤0}\\{x≥1}\end{array}\right.$且点A,B的坐标分别为(1,y),(2,$\frac{1}{x}$),则z=$\overrightarrow{OA}$$•\overrightarrow{OB}$的取值范围为[5,9].分析 z=$\overrightarrow{OA}$$•\overrightarrow{OB}$=2+2y+$\frac{1+y}{x}$,$\frac{1+y}{x}$的几何意义是点(x,y)与点C(0,-1)连线的斜率,从而作图利用线性规划求解.
解答 解:z=$\overrightarrow{OA}$$•\overrightarrow{OB}$=(1,y)•(2,$\frac{1}{x}$)=2+$\frac{1}{x}$+2y+$\frac{y}{x}$=2+2y+$\frac{1+y}{x}$,
$\frac{1+y}{x}$的几何意义是点(x,y)与点C(0,-1)连线的斜率,
作平面区域如下,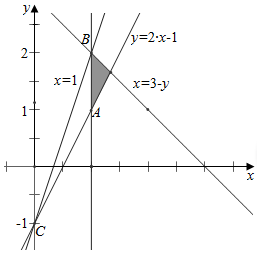 ,
,
易知kAC=$\frac{1-(-1)}{1-0}$=2,kBC=$\frac{2-(-1)}{1-0}$=3,
结合图象可得,
2+1+2≤2+2y+$\frac{1+y}{x}$≤2+4+3,
即5≤2+2y+$\frac{1+y}{x}$≤9.
故答案为:[5,9].
点评 本题考查了平面向量与线性规划问题,同时考查了数形结合的思想方法应用及转化思想的应用.

练习册系列答案
相关题目
16.在复平面内,复数z=$\frac{1+2i}{1-i}$(i是虚数单位)对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.已知函数f(x)=2sin$\frac{x}{2}$的定义域为[a,b],值域为[-1,2],则b-a的取值范围是( )
| A. | [$\frac{5π}{3}$,2π] | B. | [$\frac{4π}{3}$,2π] | C. | [$\frac{4π}{3}$,$\frac{8π}{3}$] | D. | [2π,$\frac{8π}{3}$] |