题目内容
若函数f(x)=x|x-a|在[2,+∞)上单调递增,则实数a的取值范围为 .
考点:函数单调性的性质
专题:函数的性质及应用
分析:化为分段函数,根据函数的单调性,求的a的范围,利用了数形结合的思想.
解答:
 解:∵f(x)=x|x-a|=
解:∵f(x)=x|x-a|=
,如图所示
当x≥a时,f(x)=x2-ax,函数f(x)在[2,+∞)为增函数,
当x<a时,f(x)=-x2+ax,函数f(x)在(-∞,
)为增函数,在(
,a)为减函数
又函数f(x)=x|x-a|在[2,+∞)上单调递增,
∴a≤2,
∴实数a的取值范围为(-∞,2]
故答案为:(-∞,2]
 解:∵f(x)=x|x-a|=
解:∵f(x)=x|x-a|=
|
当x≥a时,f(x)=x2-ax,函数f(x)在[2,+∞)为增函数,
当x<a时,f(x)=-x2+ax,函数f(x)在(-∞,
| a |
| 2 |
| a |
| 2 |
又函数f(x)=x|x-a|在[2,+∞)上单调递增,
∴a≤2,
∴实数a的取值范围为(-∞,2]
故答案为:(-∞,2]
点评:本题主要考查了根据函数的单调性求出参数的取值范围的问题,属于基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
函数y=|sinx|(-
<x<
)的大致图象是( )
| π |
| 2 |
| π |
| 2 |
A、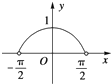 |
B、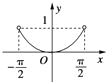 |
C、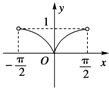 |
D、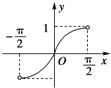 |
 如图,曲边梯形ABCD由直线x=1、x=e、x轴及曲线y=
如图,曲边梯形ABCD由直线x=1、x=e、x轴及曲线y=