题目内容
11.函数y=f(x)图象上不同两点A(x1,y1),B(x2,y2)处的切线的斜率分别是kA,kB,规定φ(A,B)=$\frac{{|{k_A}-{k_B}|}}{{|AB{|^2}}}$叫做曲线y=f(x)在点A、B之间的“平方弯曲度”.设曲线y=ex+x上不同两点A(x1,y1),B(x2,y2),且x1-x2=1,则φ(A,B)的取值范围是(0,$\frac{\sqrt{2}-1}{2}$].分析 求出y′=ex,+1,由定义求出两点A(x1,y1),B(x2,y2)之间的“平方弯曲度”,由题意可令t=e${\;}^{{x}_{1}}$-e${\;}^{{x}_{2}}$,
可设f(t)=$\frac{t}{1+(t+1)^{2}}$,t>0,求出导数和单调区间、极大值和最大值,即可得到所求范围.
解答 解:y=ex+x的导数为y′=ex+1,
kA=e${\;}^{{x}_{1}}$+1,kB=e${\;}^{{x}_{2}}$+1,
φ(A,B)=$\frac{{|{k_A}-{k_B}|}}{{|AB{|^2}}}$=$\frac{|{e}^{{x}_{1}}-{e}^{{x}_{2}}|}{({x}_{1}-{x}_{2})^{2}+({e}^{{x}_{1}}-{e}^{{x}_{2}}+{x}_{1}-{x}_{2})^{2}}$
=$\frac{|{e}^{{x}_{1}}-{e}^{{x}_{2}}|}{1+({e}^{{x}_{1}}-{e}^{{x}_{2}}+1)^{2}}$,
x1-x2=1,可得x1>x2,e${\;}^{{x}_{1}}$>e${\;}^{{x}_{2}}$,
可令t=e${\;}^{{x}_{1}}$-e${\;}^{{x}_{2}}$,
可设f(t)=$\frac{t}{1+(t+1)^{2}}$,t>0,
f′(t)=$\frac{1+(t+1)^{2}-2t(t+1)}{(1+(t+1)^{2})^{2}}$=$\frac{2-{t}^{2}}{(1+(t+1))^{2}}$,
当0<t<$\sqrt{2}$时,f′(t)>0,f(t)递增;
当t>$\sqrt{2}$时,f′(t)<0,f(t)递减.
则当t=$\sqrt{2}$处f(t)取得极大值,且为最大值$\frac{\sqrt{2}}{1+(\sqrt{2}+1)^{2}}$=$\frac{\sqrt{2}-1}{2}$.
则φ(A,B)∈(0,$\frac{\sqrt{2}-1}{2}$].
故答案为:(0,$\frac{\sqrt{2}-1}{2}$].
点评 本题考查新定义的理解和运用,考查导数的几何意义和导数的运用:求单调区间、极值和最值,考查构造法和换元法,化简整理能力,属于中档题.

| A. | f(x)是奇函数 | |
| B. | f(x)是偶函数 | |
| C. | f(x)是周期函数 | |
| D. | f(x)在$[-\frac{π}{2}+2kπ,\frac{π}{2}+2kπ](k∈z)$上为减函数 |
| A. | 64 | B. | 32 | C. | 16 | D. | 12 |
| A. | 2:3 | B. | 1:3 | C. | 1:4 | D. | 1:$\sqrt{3}$ |
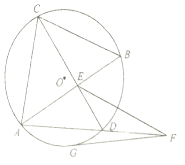 如图所示,E是园O内两条弦AB和CD的交点,过AD延长线上一点F作圆O的切线FG,G为切点,已知EF=FG.求证:EF∥CB.
如图所示,E是园O内两条弦AB和CD的交点,过AD延长线上一点F作圆O的切线FG,G为切点,已知EF=FG.求证:EF∥CB.