题目内容
在平面直角坐标系xOy中,直线l与抛物线y2=2x相交于P、Q两点,如果
•
=3,O为坐标原点.证明:直线l过定点.
| OP |
| OQ |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:设出直线的方程,同抛物线方程联立,得到关于y的一元二次方程,根据根与系数的关系表示出数量积,根据数量积等于3,做出数量积表示式中的b的值,即得到定点的坐标.
解答:
证:由题意,直线的斜率不为0,所以设l:ky=x+b,代入抛物线y2=2x,消去x得y2-2ky+2b=0,
设P(x1,y1),Q(x2,y2)
则y1+y2=2k,y1y2=2b,
∵
•
=3,
∴x1x2+y1y2=3,即(k2+1)y1y2-kb(y1+y2)+b2=3
代入得2(k2+1)b-2k2b+b2=3,解得b=-3或者b=1,
∴直线方程为ky=x-3或者ky=x+1,
故直线l过定点(3,0)或者(-1,0).
设P(x1,y1),Q(x2,y2)
则y1+y2=2k,y1y2=2b,
∵
| OP |
| OQ |
∴x1x2+y1y2=3,即(k2+1)y1y2-kb(y1+y2)+b2=3
代入得2(k2+1)b-2k2b+b2=3,解得b=-3或者b=1,
∴直线方程为ky=x-3或者ky=x+1,
故直线l过定点(3,0)或者(-1,0).
点评:本题主要考查向量的数量积的运算,以及直线与抛物线的位置关系.

练习册系列答案
相关题目
 某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:

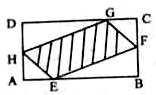 廊坊市某所中学有一块矩形空地,学校要在这块空地上修建一个内接四边形的花坛(如图所示),该花坛的四个顶点分别落在矩形的四条边上,已知 A B=a(a>2),BC=2,且 A E=A H=CF=CG,设 A E=x,花坛面积为y.
廊坊市某所中学有一块矩形空地,学校要在这块空地上修建一个内接四边形的花坛(如图所示),该花坛的四个顶点分别落在矩形的四条边上,已知 A B=a(a>2),BC=2,且 A E=A H=CF=CG,设 A E=x,花坛面积为y.