题目内容
已知p:方程
+
=1 表示焦点在y轴上的双曲线; q:方程4x2+4(m-2)x+1=0无实根又 p∨q为假,求实数m的取值范围.
| x2 |
| 2-m |
| y2 |
| m-1 |
考点:复合命题的真假
专题:简易逻辑
分析:首先,根据所给的命题,得到p:1<m<2,q:1<m<3,然后,结合条件进行求解即可.
解答:
解:根据p:方程
+
=1 表示焦点在y轴上的双曲线,得
∴
,
∴m>2,
根据q:方程4x2+4(m-2)x+1=0无实根,得
△=[4(m-2)]2-4×4×1<0,
∴1<m<3,
又 p∨q为假,
∴p,q 为假,
∴
,
∴m≤1,
∴实数m的取值范围(-∞,1].
| x2 |
| 2-m |
| y2 |
| m-1 |
∴
|
∴m>2,
根据q:方程4x2+4(m-2)x+1=0无实根,得
△=[4(m-2)]2-4×4×1<0,
∴1<m<3,
又 p∨q为假,
∴p,q 为假,
∴
|
∴m≤1,
∴实数m的取值范围(-∞,1].
点评:本题重点考查了一元二次方程根的讨论、双曲线的性质、复合命题的真假判断等知识,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
sinα=
,则sin2α-cos2α的值为( )
| ||
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知约束条件
,且目标函数z=x-2y的最大值是4,则z的最小值是( )
|
| A、-2 | B、-7 | C、-3 | D、-5 |
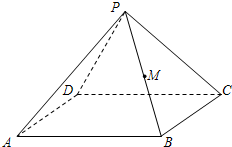 四棱锥P-ABCD中,棱长PD=a,底面ABCD是边长为a的菱形,点M为PB中点
四棱锥P-ABCD中,棱长PD=a,底面ABCD是边长为a的菱形,点M为PB中点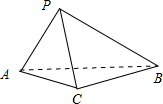 如图,已知四面体PABC的四个顶点P,A,B,C均在球O的表面上,且AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC,则球O的体积是
如图,已知四面体PABC的四个顶点P,A,B,C均在球O的表面上,且AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC,则球O的体积是