题目内容
数列{an}中，若a1=1，an+1=an+4，则下列各数中是{an}中某一项的是（ ）
| A、2007 | B、2008 |
| C、2009 | D、2010 |
考点：等差数列的通项公式
专题：计算题,等差数列与等比数列
分析：利用等差数列的定义判断，再用通项公式求解即可．
解答：
解：∵数列{an}中有a1=1，an+1=an+4，
∴数列{an}为等差数列，且a1=1，公差d=4
即通项公式为：an=4n-3，
∵4n-3=2009，4n=2012，∴n=503 且n=503是整数
故选：C
∴数列{an}为等差数列，且a1=1，公差d=4
即通项公式为：an=4n-3，
∵4n-3=2009，4n=2012，∴n=503 且n=503是整数
故选：C
点评：本题考查了等差数列的定义，通项公式，计算即可．
练习册系列答案
相关题目
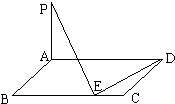如图：已知矩形ABCD中，AB=2，BC=a，若PA⊥面AC，在BC边上取点E，使PE⊥DE，则满足条件的E点有两个时，a的取值范围是（ ）| A、a＞4 | B、a≥4 |
| C、0＜a＜4 | D、0＜a≤4 |
将点M的直角坐标（
，-1）化成极坐标（ ）
| 3 |
A、（2，
| ||
B、（2，-
| ||
C、（2，
| ||
D、（2，
|
