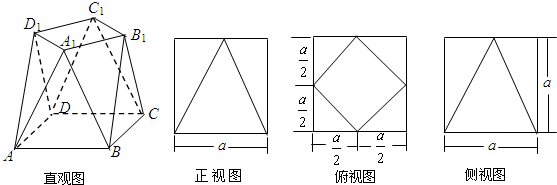
题目内容
记空间向量
=
,
=
,
=
,其中
,
,
均为单位向量.若
⊥
,且
与
,
的夹角均为θ,θ∈[0,π].有以下结论:
①
⊥(
-
);
②直线OC与平面OAB所成角等于向量
与
+
的夹角;
③若向量
+
所在直线与平面ABC垂直,则θ=60°;
④当θ=90°时,P为△ABC内(含边界)一动点,若向量
与
+
+
夹角的余弦值为
,则动点P的轨迹为圆.
其中,正确的结论有 (写出所有正确结论的序号).
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
①
| c |
| a |
| b |
②直线OC与平面OAB所成角等于向量
| c |
| a |
| b |
③若向量
| a |
| b |
④当θ=90°时,P为△ABC内(含边界)一动点,若向量
| OP |
| a |
| b |
| c |
| ||
| 3 |
其中,正确的结论有
考点:平面向量数量积的运算
专题:平面向量及应用
分析:①
•(
-
)=
•
-
•
=cosθ-cosθ=0,可得
⊥(
-
);
②当θ∈(
,π]时,直线OC与平面OAB所成角的补角等于向量
与
+
的夹角,即可判断出正误;
③向量
+
所在直线OD与平面ABC垂直于点D,又BC=AC,D为AB的中点,则CD⊥AB,可得OD⊥CD,可得AC=1=OC=OA,可得θ=60°,即可判断出正误;
④补全正方体,对角线OD与平面ABC相交于点M,点M为等边三角形的中心,可得OM=
,OP=
,MP=
.即可得出动点P的轨迹为圆,点M为圆心,MP为半径的圆.
| c |
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
②当θ∈(
| π |
| 2 |
| c |
| a |
| b |
③向量
| a |
| b |
④补全正方体,对角线OD与平面ABC相交于点M,点M为等边三角形的中心,可得OM=
| ||
| 3 |
| ||
| 2 |
| ||
| 6 |
解答:
解:①∵
•(
-
)=
•
-
•
=cosθ-cosθ=0,∴
⊥(
-
),正确;
②当θ∈[0,
]时,直线OC与平面OAB所成角等于向量
与
+
的夹角;当θ∈(
,π]时,直线OC与平面OAB所成角的补角等于向量
与
+
的夹角,因此不正确;
③向量
+
所在直线OD与平面ABC垂直于点D,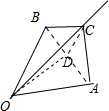 又BC=AC,D为AB的中点,则CD⊥AB,∴OD⊥CD,又OD=DA=
又BC=AC,D为AB的中点,则CD⊥AB,∴OD⊥CD,又OD=DA=
=CD,∴AC=1=OC=OA,则θ=60°,正确;
④当θ=90°时,P为△ABC内(含边界)一动点,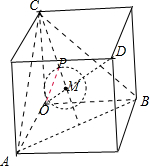 补全正方体,对角线OD与平面ABC相交于点M,点M为等边三角形的中心,OM=
补全正方体,对角线OD与平面ABC相交于点M,点M为等边三角形的中心,OM=
OD=
,
∵向量
与
+
+
(即与
)的夹角的余弦值为
,∴OP=
=
,∴MP=
=
.
∴动点P的轨迹为圆,点M为圆心,MP为半径的圆,因此正确.
其中,正确的结论有①③④.
故答案为:①③④.
| c |
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
②当θ∈[0,
| π |
| 2 |
| c |
| a |
| b |
| π |
| 2 |
| c |
| a |
| b |
③向量
| a |
| b |
 又BC=AC,D为AB的中点,则CD⊥AB,∴OD⊥CD,又OD=DA=
又BC=AC,D为AB的中点,则CD⊥AB,∴OD⊥CD,又OD=DA=
| ||
| 2 |
④当θ=90°时,P为△ABC内(含边界)一动点,
 补全正方体,对角线OD与平面ABC相交于点M,点M为等边三角形的中心,OM=
补全正方体,对角线OD与平面ABC相交于点M,点M为等边三角形的中心,OM=| 1 |
| 3 |
| ||
| 3 |
∵向量
| OP |
| a |
| b |
| c |
| OD |
| ||
| 3 |
| OM | ||||
|
| ||
| 2 |
| OP2-OM2 |
| ||
| 6 |
∴动点P的轨迹为圆,点M为圆心,MP为半径的圆,因此正确.
其中,正确的结论有①③④.
故答案为:①③④.
点评:本题考查了向量的数量积运算性质、空间线面位置关系、空间角、正方体的性质,考查了空间想象能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
如图,在△ABC中,P为中线AO上一个动点,若AO=2,则
•(
+
)的最小值是( )

| PA |
| PB |
| PC |

| A、-2 | ||
| B、-1 | ||
C、-
| ||
| D、0 |
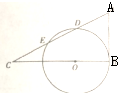 如图,圆O的圆心在Rt△ABC的直角边BC上,该圆与直角边AB相切,与斜边AC交于点D、E,AD=DE=EC,AB=
如图,圆O的圆心在Rt△ABC的直角边BC上,该圆与直角边AB相切,与斜边AC交于点D、E,AD=DE=EC,AB= 如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°,点E在BD上,且CE=DE.
如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°,点E在BD上,且CE=DE.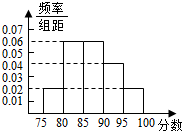 某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取50个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查: