题目内容
将参加夏令营的600名学生编号：001，002，…，600，采用系统抽样方法抽取一个容量为50的样本，且随机抽得的号码为003，这600名学生分住在三个营区，从001到300在第Ⅰ营区，从301到483在第Ⅱ营区，从484到600在Ⅲ营区，三个营区被抽中的人数依次为（ ）
| A、25，16，9 |
| B、26，16，8 |
| C、25，17，8 |
| D、24，17，9 |
考点：分层抽样方法
专题：概率与统计
分析：先计算组距是多少，再利用第一个号码为003，列出不等式3+12（k-1）≤300，求出对应各营区被抽中的人数．
解答：
解：从600名学生中抽取容量为50的样本，组距是
=12；
又抽得第一个号码为003，
∵3+12（k-1）≤300，∴k≤
+1，且
+1的整数部分是25，
∴从001到300应抽取的人数是25；
又∵3+12（k-1）≤483，∴k≤41，
∴从301到483应抽取的人数是41-25=16；
∴从484到600应抽取的人数是50-41=9；
即三个营区被抽中的人数依次为25、16、9．
故选：A．
| 600 |
| 50 |
又抽得第一个号码为003，
∵3+12（k-1）≤300，∴k≤
| 99 |
| 4 |
| 99 |
| 4 |
∴从001到300应抽取的人数是25；
又∵3+12（k-1）≤483，∴k≤41，
∴从301到483应抽取的人数是41-25=16；
∴从484到600应抽取的人数是50-41=9；
即三个营区被抽中的人数依次为25、16、9．
故选：A．
点评：本题考查了分层抽样方法的应用问题，也考查了系统抽样方法的应用问题，是基础题目．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
设函数f（x）=loga（x-a+2）在区间（1，+∞）上恒为正值，则实数a的取值范围是（ ）
| A、（1，2] | ||
| B、（1，2） | ||
| C、（0，1）∪（1，2） | ||
D、(1，
|
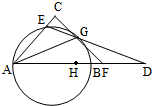过以AB为直径的圆上C点作直线交圆于E点，交AB延长线于D点，过C点作圆的切线交AD于F点，交AE延长线于G点，且GA=GF．（Ⅰ）求证CA=CD；
（Ⅱ）设H为AD的中点，求证BH•BA=BF•BD．
设复数z满足（2-i）z=3+i则z=（ ）
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
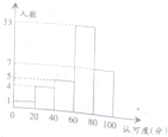某校为了了解新的一轮数改墨水有效性的“认可度”，在全校师生（可认为很多人）进行了“认可度”的问卷调查，现随机抽查50名师生，对他们的“认可度”的问卷调查，现随机抽查50名师生，对他们的“认可度”统计分析得如图：