题目内容
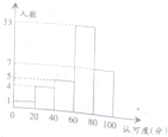 某校为了了解新的一轮数改墨水有效性的“认可度”,在全校师生(可认为很多人)进行了“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”统计分析得如图:
某校为了了解新的一轮数改墨水有效性的“认可度”,在全校师生(可认为很多人)进行了“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”统计分析得如图:(1)求这50名师生的“认可度”的平均值(每一区间取中点值计算);
(2)求从这50名师生中任取一人的“认可度”的分数在60(含)分以上的概率;
(3)以这50名师生的“认可度”来估计全校师生总体“认可度”的评价,若从中随机抽取4人的“认可度”,用ξ表示抽到的“认可度”分数在60(含)分以上的人数,求ξ的分布列与整数期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(1)根据频率分布直方图和平均数的求法求出50名师生的“认可度”的平均值即可.
(2)由频率分布图知这50名师生中“认可度”的分数在60(含)分以上的人数为40人,由此能求出这50名师生中任取一人的“认可度”的分数在60(含)分以上的概率.
(3)由已知得ξ的可能取值为0,1,2,3,4,分别求出相应的概率,由此能求出ξ的分布列与整数期望.
(2)由频率分布图知这50名师生中“认可度”的分数在60(含)分以上的人数为40人,由此能求出这50名师生中任取一人的“认可度”的分数在60(含)分以上的概率.
(3)由已知得ξ的可能取值为0,1,2,3,4,分别求出相应的概率,由此能求出ξ的分布列与整数期望.
解答:
解:(1)由频率分布直方图,得:
=
(10×1+30×4+50×5+70×33+90×7)=66.4.
∴这50名师生的“认可度”的平均值为66.4.
(2)由频率分布图知:
这50名师生中“认可度”的分数在60(含)分以上的人数为:33+7=40人,
∴这50名师生中任取一人的“认可度”的分数在60(含)分以上的概率为:
P=
=
.
(3)由已知得ξ的可能取值为0,1,2,3,4,
P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
,
P(ξ=4)=
=
,
∴ξ的分布列为:
Eξ=0×
+1×
+2×
+3×
≈2.
. |
| x |
| 1 |
| 50 |
∴这50名师生的“认可度”的平均值为66.4.
(2)由频率分布图知:
这50名师生中“认可度”的分数在60(含)分以上的人数为:33+7=40人,
∴这50名师生中任取一人的“认可度”的分数在60(含)分以上的概率为:
P=
| 40 |
| 50 |
| 4 |
| 5 |
(3)由已知得ξ的可能取值为0,1,2,3,4,
P(ξ=0)=
| ||
|
| 21 |
| 23030 |
P(ξ=1)=
| ||||
|
| 48 |
| 2303 |
P(ξ=2)=
| ||||
|
| 351 |
| 2303 |
P(ξ=3)=
| ||||
|
| 988 |
| 2303 |
P(ξ=4)=
| ||
|
| 9139 |
| 23030 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 21 |
| 23030 |
| 48 |
| 2303 |
| 351 |
| 2303 |
| 988 |
| 2303 |
点评:本题考查频率分布直方图的应用,考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
将参加夏令营的600名学生编号:001,002,…,600,采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003,这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到483在第Ⅱ营区,从484到600在Ⅲ营区,三个营区被抽中的人数依次为( )
| A、25,16,9 |
| B、26,16,8 |
| C、25,17,8 |
| D、24,17,9 |
已知全集U={1,2,3,4,5},集合A={1,2,3},B={2,3,5},则∁U(A∩B)=( )
| A、{1,4,5} |
| B、{1,2,3} |
| C、{3,4} |
| D、{4} |
从1,2,3,4中取任意两个不同的数,则取出的2个数之差的绝对值为3的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在等比数列{an}中,已知a1=2,a2a3=32,则数列{an}的前6项和S6=( )
| A、62 | B、64 |
| C、126 | D、128 |
函数f(x)是定义域为R的奇函数,当x>0时,f(x)=-x+1,则当x<0时,f(x)=( )
| A、-x-1 | B、-x+1 |
| C、x+1 | D、x-1 |