题目内容
(2011•浙江)设F1,F2分别为椭圆 +y2=1的焦点,点A,B在椭圆上,若
+y2=1的焦点,点A,B在椭圆上,若 =5
=5 ;则点A的坐标是 _________ .
;则点A的坐标是 _________ .
 +y2=1的焦点,点A,B在椭圆上,若
+y2=1的焦点,点A,B在椭圆上,若 =5
=5 ;则点A的坐标是 _________ .
;则点A的坐标是 _________ .(0,±1)
方法1:直线F1A的反向延长线与椭圆交于点B'
又∵
由椭圆的对称性,得
设A(x1,y1),B'(x2,y2)
由于椭圆 的a=
的a= ,b=1,c=
,b=1,c=
∴e= ,F1(
,F1( ,0).
,0).
∵

从而有:

由于 ≤x1,x2
≤x1,x2 ,
,
∴ ,
, ,
,
即 =5×
=5×
 =5
=5 . ①
. ①
又∵三点A,F1,B′共线,
∴( ,y1﹣0)=5(﹣
,y1﹣0)=5(﹣ ﹣x2,0﹣y2)
﹣x2,0﹣y2)
∴ .②
.②
由①+②得:x1=0.
代入椭圆的方程得:y1=±1,
∴点A的坐标为(0,1)或(0,﹣1)
方法2:因为F1,F2分别为椭圆 的焦点,则
的焦点,则 ,设A,B的坐标分别为A(xA,yA),B(xB,yB),
,设A,B的坐标分别为A(xA,yA),B(xB,yB),
若 ;则
;则 ,所以
,所以 ,
,
因为A,B在椭圆上,所以 ,代入解得
,代入解得 或
或 ,
,
故A(0,±1).
又∵

由椭圆的对称性,得

设A(x1,y1),B'(x2,y2)
由于椭圆
 的a=
的a= ,b=1,c=
,b=1,c=
∴e=
 ,F1(
,F1( ,0).
,0).∵


从而有:

由于
 ≤x1,x2
≤x1,x2 ,
,∴
 ,
, ,
,即
 =5×
=5×
 =5
=5 . ①
. ①又∵三点A,F1,B′共线,

∴(
 ,y1﹣0)=5(﹣
,y1﹣0)=5(﹣ ﹣x2,0﹣y2)
﹣x2,0﹣y2)∴
 .②
.②由①+②得:x1=0.
代入椭圆的方程得:y1=±1,
∴点A的坐标为(0,1)或(0,﹣1)
方法2:因为F1,F2分别为椭圆
 的焦点,则
的焦点,则 ,设A,B的坐标分别为A(xA,yA),B(xB,yB),
,设A,B的坐标分别为A(xA,yA),B(xB,yB),若
 ;则
;则 ,所以
,所以 ,
,因为A,B在椭圆上,所以
 ,代入解得
,代入解得 或
或 ,
,故A(0,±1).

练习册系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,,右顶点为A,上顶点为B.已知
,,右顶点为A,上顶点为B.已知 =
=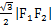 .
. ,经过点
,经过点 的直线
的直线 与该圆相切与点M,
与该圆相切与点M, =
= .求椭圆的方程.
.求椭圆的方程.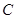 过点
过点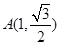 ,两焦点为
,两焦点为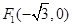 、
、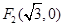 ,
,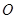 是坐标原点,不经过原点的直线
是坐标原点,不经过原点的直线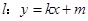 与椭圆交于两不同点
与椭圆交于两不同点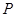 、
、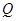 .
.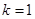 时,求
时,求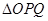 面积的最大值;
面积的最大值;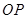 、
、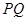 、
、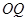 的斜率依次成等比数列,求直线
的斜率依次成等比数列,求直线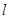 的斜率
的斜率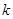 .
. :
: 的一个焦点为
的一个焦点为 ,离心率为
,离心率为 .设
.设 是椭圆
是椭圆 的直线
的直线 交椭圆于
交椭圆于 ,
, 两点.
两点. 的最大值.
的最大值.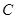 :
: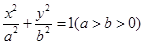 经过点
经过点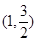 ,其离心率
,其离心率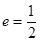 .
.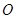 作不与坐标轴重合的直线
作不与坐标轴重合的直线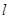 交椭圆
交椭圆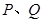 两点,过
两点,过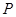 作
作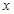 轴的垂线,垂足为
轴的垂线,垂足为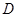 ,连接
,连接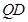 并延长交椭圆
并延长交椭圆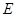 ,试判断随着
,试判断随着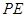 与
与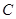 的中心在原点,焦点在
的中心在原点,焦点在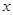 轴上,离心率为
轴上,离心率为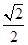 ,它的一个焦点恰好与抛物线
,它的一个焦点恰好与抛物线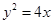 的焦点重合.
的焦点重合.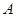 ,过点
,过点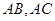 ,若直线
,若直线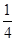 ,直线
,直线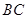 是否一定经过一定点?若经过,求出该定点坐标;若不经过,请说明理由.
是否一定经过一定点?若经过,求出该定点坐标;若不经过,请说明理由.
 ,离心率等于
,离心率等于 ,则椭圆的方程是( )
,则椭圆的方程是( ) 



 上的动点,点D是P在
上的动点,点D是P在 轴上投影,M为PD上一点,且
轴上投影,M为PD上一点,且 .
.
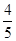 的直线被C所截线段的长度.
的直线被C所截线段的长度.