题目内容
3.抛物线y=2x2上两点A(x1,y1),B(x2,y2)关于直线y=x+m对称,且x1•x2=-$\frac{3}{4}$,则实数m的值为2.分析 先利用条件得出A、B两点连线的斜率k,再利用A、B两点的中点在直线y=x+m求出关于m以及x2,x1的方程,再与已知条件联立求出实数m的值.
解答 解:由题意,$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=-1,y2-y1=2(x22-x12),
∴x1+x2=-$\frac{1}{2}$,
$(\frac{{{x_2}+{x_1}}}{2},\frac{{{y_2}+{y_1}}}{2})$在直线y=x+m上,即$\frac{{{y_2}+{y_1}}}{2}=\frac{{{x_2}+{x_1}}}{2}+m,{y_2}+{y_1}={x_2}+{x_1}+2m$,
所以有2(x22+x12)=x2+x1+2m,即2[(x2+x1)2-2x2x1]=x2+x1+2m,
∴2m=4,∴m=2,
故答案为2.
点评 本题是对直线与抛物线位置关系以及点与直线位置的综合考查.当两点关于已知直线对称时,有两条结论,一是两点的中点在已知直线上;二是两点的连线与已知直线垂直.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
13.若以等边三角形ABC的顶点A,B为焦点的双曲线恰好过BC的中点,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{3}+1$ |
14.“a(a-1)≤0”是“方程x2+x-a=0有实数根”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
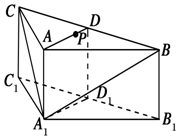 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.