题目内容
8.在△ABC中,角A,B,C的对边分别为a,b,c,∠A,∠B,∠C的大小成等差数列,且a=1,$b=\sqrt{3}$.则∠A的大小为( )| A. | $\frac{π}{6}$或$\frac{5π}{6}$ | B. | $\frac{π}{3}$或$\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
分析 由∠A、∠B、∠C的大小成等差数列,利用等差数列的性质及内角和定理求出B的度数,确定出A+C的度数,利用正弦定理列出关系式,将a,b,sinB的值代入求出sinA的值,确定出A的度数即可得解.
解答 解:∵A,B,C成等差数列,
∴A+C=2B=π-B,
解得:B=$\frac{π}{3}$,A+C=$\frac{2π}{3}$,
由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$,a=1,b=$\sqrt{3}$,
∴$\frac{1}{sinA}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2,即sinA=$\frac{1}{2}$,
又∵0<A<$\frac{2π}{3}$,
∴A=$\frac{π}{6}$.
故选:C.
点评 此题考查了正弦定理,正弦函数的定义域与值域,等差数列的性质,熟练掌握正弦定理是解本题的关键,属于基础题.

练习册系列答案
相关题目
13.若以等边三角形ABC的顶点A,B为焦点的双曲线恰好过BC的中点,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{3}+1$ |
20.已知f(x)=lnx-e-x,a=2e,b=ln2,c=log2e(其中e为自然对数的底数)则f(a),f(b),f(c)的大小顺序为( )
| A. | f(a)<f(b)<f(c) | B. | f(a)<f(c)<f(b) | C. | f(b)<f(c)<f(a) | D. | f(c)<f(b)<f(a) |
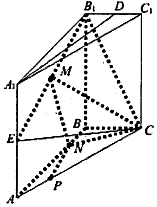 已知在三棱柱ABC-A1B1C1中,B1B⊥平面ABC,∠ABC=90°,B1B=AB=2BC=4,D、E分别是B1C1,A1A的中点.
已知在三棱柱ABC-A1B1C1中,B1B⊥平面ABC,∠ABC=90°,B1B=AB=2BC=4,D、E分别是B1C1,A1A的中点.