题目内容
9.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π)的图象如图所示,则f($\frac{5π}{12}$)=-$\frac{1}{2}$.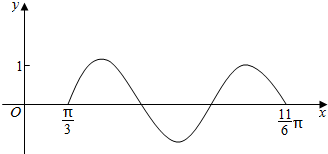
分析 利用三角函数的图象,求出函数的周期,即可得到ω的值,由($\frac{π}{3}$,0)在函数图象上,可解得:φ=kπ-$\frac{2π}{3}$,k∈Z,结合范围|φ|<π,解得φ的值,利用诱导公式即可求解f($\frac{5π}{12}$)的值.
解答 解:∵由函数的图象可知:$\frac{3}{2}$T=$\frac{11π}{6}-\frac{π}{3}$,解得:T=π=$\frac{2π}{ω}$,
∴ω=2.
∵($\frac{π}{3}$,0)在函数图象上,可得:sin(2×$\frac{π}{3}$+φ)=0,
∴解得:φ=kπ-$\frac{2π}{3}$,k∈Z,
∵|φ|<π,
∴φ=$\frac{π}{3}$,可得:f(x)=sin(2x+$\frac{π}{3}$),
∴f($\frac{5π}{12}$)=sin(2×$\frac{5π}{12}$+$\frac{π}{3}$)=-$\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查学生的视图与用图能力,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 正方体ABCD-A1B1C1D1的棱长为2,E为棱CC1的中点.
正方体ABCD-A1B1C1D1的棱长为2,E为棱CC1的中点.