题目内容
14.已知tan2θ=-2$\sqrt{2}$,π<2θ<2π,化简$\frac{2co{s}^{2}θ-sinθ-1}{\sqrt{2}sin(θ+\frac{π}{4})}$=3+2$\sqrt{2}$.分析 通过正切的倍角公式根据tan2θ求出tanθ的值;先用正弦两角和公式对原式进行化简,再tanθ代入即可得到答案.
解答 解:tan2θ=$\frac{2tanθ}{1-{tan}^{2}θ}$=-2$\sqrt{2}$,即$\sqrt{2}$tan2θ-tanθ-$\sqrt{2}$=0,
又∵π<2θ<2π,可得$\frac{π}{2}$<θ<π,∴tanθ=$-\frac{\sqrt{2}}{2}$,
$\frac{2co{s}^{2}\frac{θ}{2}-sinθ-1}{\sqrt{2}sin(θ+\frac{π}{4})}$=$\frac{cosθ-sinθ}{sinθ+cosθ}$=$\frac{1-tanθ}{1+tanθ}$=$\frac{1+\frac{\sqrt{2}}{2}}{1-\frac{\sqrt{2}}{2}}$=$\frac{2+\sqrt{2}}{2-\sqrt{2}}$=3+$\sqrt{2}$.
故答案为:3+2$\sqrt{2}$.
点评 本题主要考查三角函数中的两角和公式运用,在求tanθ的过程中,要注意定义域,属中档题.

练习册系列答案
相关题目
3.非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足$\sqrt{3}$|$\overrightarrow{a}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则向量$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{b}$-$\overrightarrow{a}$夹角的余弦值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
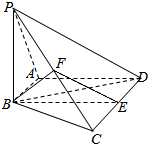 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是棱CD和PC的中点.