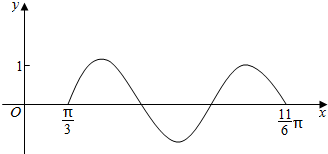
题目内容
4.三角形ABC中,sinBcosC=cosBcos(A+B),三角形ABC的形状为钝角三角形.分析 利用诱导公式化简表达式,然后求解即可.
解答 解:三角形ABC中,sinBcosC=cosBcos(A+B),
可得sinBcosC=cosBcos(π-C)=-cosBcosC,
化简为:sinB=-cosB,
tanB=-1,可得B=135°,
三角形ABC的形状为:钝角三角形.
故答案为:钝角三角形.
点评 本题考查三角形的形状的判断,考查计算能力.

练习册系列答案
相关题目
12.已知函数f(x)=3tanωx+1,若对任意x1,x2∈(-$\frac{π}{3}$,$\frac{π}{4}$)且x1≠x2,均有[f(x1)-f(x2)](x1-x2)<0成立.则实数ω的取值范围是( )
| A. | -$\frac{3}{2}$≤ω≤$\frac{3}{2}$ | B. | -$\frac{3}{2}$≤ω≤0 | C. | -2≤ω<0 | D. | -2≤ω≤2 |