题目内容
我们将侧棱和底面边统称为棱，则三棱锥有4个面，6条棱，4个顶点，如果面数记作F，棱数记作E，顶点数记作V，那么F，E，V之间有什么关系？再用三棱柱，四棱台检验你得到的关系式，你知道这是个什么公式？
考点：归纳推理
专题：计算题,推理和证明
分析：通过列举正方体、三棱柱、三棱锥的面数F、顶点数V和棱数E，得到规律：V+F-E=2，进而发现此公式对任意凸多面体都成立，由此得到本题的答案．
解答：
解：凸多面体的面数为F、顶点数为V和棱数为E，举例如下
①正方体：F=6，V=8，E=12，得V+F-E=8+6-12=2；
②三棱柱：F=5，V=6，E=9，得V+F-E=5+6-9=2；
③三棱锥：F=4，V=4，E=6，得V+F-E=4+4-6=2．
根据以上几个例子，猜想：凸多面体的面数F、顶点数V和棱数E满足如下关系：V+F-E=2
再通过举四棱锥、六棱柱、…等等，发现上述公式都成立．
因此归纳出一般结论：V+F-E=2
这个是欧拉式．
①正方体：F=6，V=8，E=12，得V+F-E=8+6-12=2；
②三棱柱：F=5，V=6，E=9，得V+F-E=5+6-9=2；
③三棱锥：F=4，V=4，E=6，得V+F-E=4+4-6=2．
根据以上几个例子，猜想：凸多面体的面数F、顶点数V和棱数E满足如下关系：V+F-E=2
再通过举四棱锥、六棱柱、…等等，发现上述公式都成立．
因此归纳出一般结论：V+F-E=2
这个是欧拉式．
点评：本题由几个特殊多面体，观察它们的顶点数、面数和棱数，归纳出一般结论，得到欧拉公式，着重考查了归纳推理和凸多面体的性质等知识，属于基础题．
练习册系列答案
相关题目
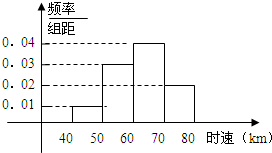已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示．
如图，四棱柱ABCD-A1B1C1D1中，A1D⊥平面ABCD，底面ABCD是边长为l的正方形，侧棱AA1=2．