题目内容
已知|
|=
，|
|=2，＜
，
＞=30°，求|
+
|，|
-
|．
| a |
| 3 |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：由向量的数量积的定义，得到向量a，b的数量积，可求|
+
|，|
-
|的平方，注意运用向量的平方即为模的平方，即可得到结果．
| a |
| b |
| a |
| b |
解答：
解：由于|
|=
，|
|=2，＜
，
＞=30°，
则
•
=|
|•|
|•cos30°=2
×
=3．
则|
+
|2=
2+
2+2
•
=3+4+2×3=13，
即有|
+
|=
；
又|
-
|2=
2+
2-2
•
=3+4-2×3=1，|
即有
-
|=1．
| a |
| 3 |
| b |
| a |
| b |
则
| a |
| b |
| a |
| b |
| 3 |
| ||
| 2 |
则|
| a |
| b |
| a |
| b |
| a |
| b |
即有|
| a |
| b |
| 13 |
又|
| a |
| b |
| a |
| b |
| a |
| b |
即有
| a |
| b |
点评：本题考查平面向量的运用，考查向量的数量积的定义和性质：向量的平方即为模的平方，考查运算能力，属于基础题．
练习册系列答案
相关题目
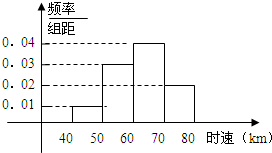已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示．
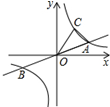如图，已知直线y=