题目内容
16.点P为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$右支上的一点,其左、右焦点分别为F1,F2,若△PF1F2的内切圆I与x轴相切于点A,过F2作PI的垂线,重足为B,O为坐标原点,那么$\frac{{|{OA}|}}{{|{OB}|}}$的值为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{b}{a}$ | D. | $\frac{a}{b}$ |
分析 根据题意,利用切线长定理,再利用双曲线的定义,把|PF1|-|PF2|=2a,转化为|AF1|-|AF2|=2a,从而求得点H的横坐标.再在三角形PCF2中,由题意得,它是一个等腰三角形,从而在三角形F1CF2中,利用中位线定理得出OB,从而解决问题.
解答 解:F1(-c,0)、F2(c,0),内切圆与x轴的切点是点A
∵|PF1|-|PF2|=2a,及圆的切线长定理知,
|AF1|-|AF2|=2a,设内切圆的圆心横坐标为x,
则|(x+c)-(c-x)|=2a
∴x=a;
|OA|=a,
在△PCF2中,由题意得,F2B⊥PI于B,延长交F1F2于点C,利用△PCB≌△PF2B,可知|PC|=|PF2|,
∴在三角形F1CF2中,有:
丨OB丨=$\frac{1}{2}$丨CF1丨=$\frac{1}{2}$(丨PF1丨-丨PC丨)=$\frac{1}{2}$(丨PF1丨-丨PF2丨)=$\frac{1}{2}$×2a=a.
∴|OB|=|OA|.
$\frac{{|{OA}|}}{{|{OB}|}}$=1
故选A.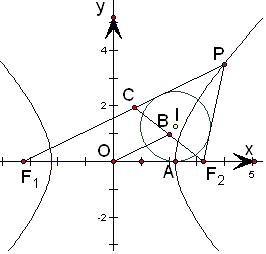
点评 本题考查双曲线的定义、切线长定理.解答的关键是充分利用平面几何的性质,如三角形内心的性质等,属于中档题.

练习册系列答案
相关题目
6.已知sin($\frac{3π}{2}$-θ)+3cos(π-θ)=sin(-θ),则sinθcosθ+cos2θ=( )
| A. | -$\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{17}$ |
7.已知向量|$\overrightarrow{OA}$|=3,|$\overrightarrow{OB}$|=2,$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,若$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°,且$\overrightarrow{OC}$⊥$\overrightarrow{AB}$,则实数$\frac{m}{n}$的值为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | 6 | D. | 4 |
11.已知(1+x)(1-2x)6=a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,则a3=( )
| A. | 220 | B. | 350 | C. | 380 | D. | 410 |
1.已知数列{an}满足a2=2,2an+1=an,则数列{an}的前6项和S6等于( )
| A. | $\frac{63}{16}$ | B. | $\frac{63}{12}$ | C. | $\frac{63}{8}$ | D. | $\frac{63}{4}$ |