题目内容
11.已知(1+x)(1-2x)6=a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,则a3=( )| A. | 220 | B. | 350 | C. | 380 | D. | 410 |
分析 由(1+x)(1-2x)6=[(x-1)+2][2(x-1)+1]6,可得[(x-1)+2][2(x-1)+1]6 =a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,求得a3的值.
解答 解:由(1+x)(1-2x)6=[(x-1)+2][2(x-1)+1]6,
(1+x)(1-2x)6=a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,
∴[(x-1)+2][2(x-1)+1]6 =a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,
∴a3=C6222+2C6323=60+320=380,
故选:C.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.点P为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$右支上的一点,其左、右焦点分别为F1,F2,若△PF1F2的内切圆I与x轴相切于点A,过F2作PI的垂线,重足为B,O为坐标原点,那么$\frac{{|{OA}|}}{{|{OB}|}}$的值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{b}{a}$ | D. | $\frac{a}{b}$ |
13.圆(x-1)2+(y+1)2=10的半径为( )
| A. | (1,-1) | B. | (-1,1) | C. | $\sqrt{10}$ | D. | 10 |
14.某多面体的三视图如下图所示(网格纸上小正方形的边长为1),则该多面体的表面积为( )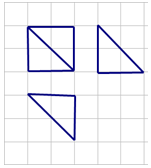

| A. | $8+4\sqrt{2}$ | B. | $6+4\sqrt{2}$ | C. | 12 | D. | $8+5\sqrt{2}$ |
