题目内容
若函数f（x）是定义在R上的奇函数，且f（x）在（0，+∞）上的最大值为5，则关于f（x）在（-∞，0）上，下列说法正确的是（ ）
| A、最大值为5 |
| B、最小值为5 |
| C、最大值为-5 |
| D、最小值为-5 |
考点：抽象函数及其应用
专题：函数的性质及应用
分析：根据函数奇偶性和单调性，最值之间的关系即可得到结论．
解答：
解：∵函数f（x）是定义在R上的奇函数，且f（x）在（0，+∞）上的最大值为5，
设x＞0时，函数的最大值为f（a）=5，
即f（x）≤f（a），
则-x＜0，此时-f（x）≥-f（a），
∵函数f（x）是奇函数，则f（-x）≥-f（a）=-5，
即f（x）在（-∞，0）上有最小值为-5，
故选：D
设x＞0时，函数的最大值为f（a）=5，
即f（x）≤f（a），
则-x＜0，此时-f（x）≥-f（a），
∵函数f（x）是奇函数，则f（-x）≥-f（a）=-5，
即f（x）在（-∞，0）上有最小值为-5，
故选：D
点评：本题主要考查奇函数的应用，利用函数奇偶性和单调性之间的关系是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
下列各式不能化为
的是（ ）
| AD |
A、
| ||||||||
B、（
| ||||||||
C、（
| ||||||||
D、-
|
若f（x）=3sin（ωx+φ）（ω＞0，|φ|＜
）的周期为π且图象关于x=
对称，则（ ）
| π |
| 2 |
| 2π |
| 3 |
A、f（x）的图象过点（0，
| ||||
B、f（x）在[
| ||||
| C、将f（x）的图象向右平移|φ|个单位得到函数y=3sinωx的图象 | ||||
D、f（x）的一个对称中心是（
|
函数y=3sin（x+
）的一条对称轴方程为（ ）
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
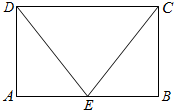如图，矩形ABCD中，点E为边AB的中点，若在矩形ABCD内部随机取一个点Q，则点Q取自△AED或△BEC内部的概率等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
tan12°-
| ||
| sin6°sin84° |
| A、4 | B、8 | C、16 | D、32 |
A={x|y=
}，B={y|y=
}，则A∪B=（ ）
| 2x-x2 |
| x2+1 |
| x2 |
| A、（1，2] |
| B、[0，1）∪（1，2] |
| C、[0，+∞] |
| D、[0，2] |