题目内容
已知双曲线
-
=1,其右焦点为F,P其上一点,点M满足|
|=1,
•
=0,则|
|的最小值为 .
| x2 |
| 9 |
| y2 |
| 16 |
. |
| MF |
. |
| MF |
| MP |
| MP |
考点:双曲线的简单性质
专题:数形结合,平面向量及应用,圆锥曲线中的最值与范围问题
分析:画出图形,结合图形,得出在Rt△FPM中,要使直角边|
|最小,只需|
|最小,求出|
|的最小值,即得|
|的最小值.
| MP |
| FP |
| FP |
| MP |
解答:
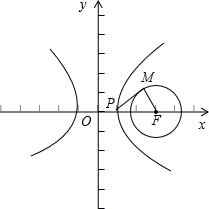 解:∵|
解:∵|
|=1,∴点M是以点F(5,0)为圆心,1为半径的单位圆;
不妨设P为双曲线右支上的任一点,
∵
•
=0,∴
⊥
,
∴△PMF为直角三角形,且∠FMP=90°,|
|为该直角三角形的斜边长;
∵P为双曲线
-
=1上的点,
在Rt△FPM中,要使直角边|
|最小,由于|
|=1,
只需|
|最小,
∵当点P为双曲线C的右支与x轴的交点时,|
|最小,此时P(3,0).
∴|
|=
=
,如图所示;
∴|
|的最小值为
.
故答案为:
.
 解:∵|
解:∵|| MF |
不妨设P为双曲线右支上的任一点,
∵
| MF |
| MP |
| MF |
| MP |
∴△PMF为直角三角形,且∠FMP=90°,|
| FP |
∵P为双曲线
| x2 |
| 9 |
| y2 |
| 16 |
在Rt△FPM中,要使直角边|
| MP |
| MF |
只需|
| FP |
∵当点P为双曲线C的右支与x轴的交点时,|
| FP |
∴|
| MP |
| (5-3)2-12 |
| 3 |
∴|
| MP |
| 3 |
故答案为:
| 3 |
点评:本题考查了平面向量的应用问题,也考查了双曲线的定义与几何性质的应用问题,考查了圆的定义与性质的应用问题,是综合题.

练习册系列答案
相关题目
在区间(0,+∞)上是减函数的是( )
| A、y=2x | ||
B、y=log
| ||
| C、y=2x | ||
| D、y=x2 |
已知A(2,1),B(3,5),把
按向量(3,2)平移后得到一个新向量
,那么下面各向量中能与
垂直的是( )
| AB |
| CD |
| CD |
| A、(-3,-2) | ||||
B、(
| ||||
| C、(-4,1) | ||||
| D、(0,-2) |
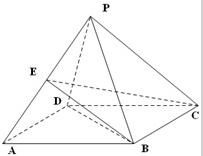 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=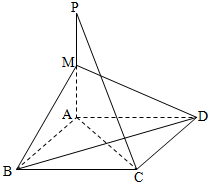 如图,四边形ABCD是菱形,PA⊥平面ABCD,M为PA的中点.
如图,四边形ABCD是菱形,PA⊥平面ABCD,M为PA的中点.