题目内容
如图,已知抛物线C1:x2+by=b2经过椭圆C2: 
+
=1(a>b>0)的两个焦点.
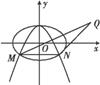
(1)求椭圆C2的离心率;
(2)设点Q(3,b),又M,N为C1与C2不在y轴上的两个交点,若△QMN的重心在抛物线C1上,求C1和C2的方程.
解:(1)因为抛物线C1经过椭圆C2的两个焦点F1(-c,0),F2(c,0),
所以c2+b×0=b2,
即c2=b2.
又a2=b2+c2=2c2,
所以椭圆C2的离心率e=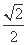
.
(2)由(1)可知a2=2b2,
椭圆C2的方程为
+=1.
联立抛物线C1的方程x2+by=b2,
得2y2-by-b2=0,
解得y=-
或y=b(舍去),
所以x=±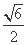
b,
即M（
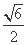b,- ）,N（b,- ）,
所以△QMN的重心坐标为(1,0).
因为重心在C1上,
所以12+b×0=b2,得b=1.
所以a2=2.
所以抛物线C1的方程为x2+y=1,
椭圆C2的方程为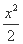
+y2=1.
练习册系列答案
相关题目
-
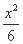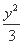=1的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r=( )
(B)2 (C)3 (D)6
+
=1(a>b>0)的左焦点为F,离心率为
,过点F且与x轴垂直的直线被椭圆截得的线段长为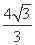
.
·
+
·
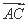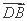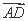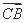=8,求k的值.
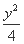=1有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
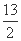(B)a2=13
(D)b2=2
y (B)x2=
y
,在y轴上截得线段长为2
.
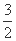x (B)y=±
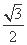x
x (D)y=±
