题目内容
数列{an}的前n项和为Sn=2an-2，数列{bn}是首项为a1，公差不为零的等差数列，且b1，b3，b11成等比数列．
（1）求数列{an}与{bn}的通项公式；
（2）求数列{
}的前n项和Tn．
（1）求数列{an}与{bn}的通项公式；
（2）求数列{
| bn |
| an |
考点：数列的求和,等比数列的性质
专题：等差数列与等比数列
分析：（1）由已知条件利用公式an=
能求出数列{an}的通项公式；由b1，b3，b11成等比数列，能求出公差d=3，由此能求出数列{bn }的通项公式．
（2）令Tn=
+
+
+…+
，由此利用错位相减求和法能求出数列{
}的前n项和Tn．
|
（2）令Tn=
| b1 |
| a1 |
| b2 |
| a2 |
| b3 |
| a3 |
| bn |
| an |
| bn |
| an |
解答：
解：（1）当n≥2时，an=Sn-Sn-1
=（2an-2）-（2an-1-2）=2an-2an-1，
∴an=2an-1，
又a1=S1=2a1-2，解得a1=2，
∴数列{an}是以2为首项，公比为2的等比数列，
∴数列{an}的通项公式为an=2n．
b1=a1=2，设公差为d，
则由b1，b3，b11成等比数列，得（2+2d）2=2×（2+10d），…（4分）
解得d=0（舍去）或d=3，
∴数列{bn }的通项公式为bn=3n-1．…（6分）
（2）令Tn=
+
+
+…+
=
+
+
+…+
，
∴2Tn=2+
+
+…+
，
两式相减得Tn=2+
+
+…+
-
，
∴Tn=2+
-
=5-
．…（12分）
=（2an-2）-（2an-1-2）=2an-2an-1，
∴an=2an-1，
又a1=S1=2a1-2，解得a1=2，
∴数列{an}是以2为首项，公比为2的等比数列，
∴数列{an}的通项公式为an=2n．
b1=a1=2，设公差为d，
则由b1，b3，b11成等比数列，得（2+2d）2=2×（2+10d），…（4分）
解得d=0（舍去）或d=3，
∴数列{bn }的通项公式为bn=3n-1．…（6分）
（2）令Tn=
| b1 |
| a1 |
| b2 |
| a2 |
| b3 |
| a3 |
| bn |
| an |
=
| 2 |
| 2 |
| 5 |
| 22 |
| 8 |
| 23 |
| 3n-1 |
| 2n |
∴2Tn=2+
| 5 |
| 2 |
| 8 |
| 22 |
| 3n-1 |
| 2n-1 |
两式相减得Tn=2+
| 3 |
| 2 |
| 3 |
| 22 |
| 3 |
| 2n-1 |
| 3n-1 |
| 2n |
∴Tn=2+
| ||||
1-
|
| 3n-1 |
| 2n |
=5-
| 3n+5 |
| 2n |
点评：本题考查数列的通项公式的求法，考查数列的前n项和的求法，解题时要认真审题，注意错位相减求和法的合理运用．
练习册系列答案
相关题目
在等比数列{an}中，已知a1=1，a4=8，则a6=（ ）
| A、16 | B、16或-16 |
| C、32 | D、32或-32 |
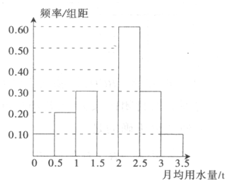我国是世界上严重缺水的国家之一，城市缺水问题较为突出．某市为了节约生活用水，计划在本市试行居民生活用水定额管理（即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费，超过a的部分按照议价收费）．为了较为合理地确定出这个标准，通过抽样获得了 100位居民某年的月均用水量（单位：t），制作了频率分布直方图，
如图，设A是单位圆和x轴正半轴的交点，P，Q是单位圆上两点，O是坐标原点，且P（