题目内容
在平面直角坐标系中,已知O为坐标原点,点A的坐标为(a,b),点B的坐标为(cosωx,sinωx),其中a2+b2≠0且ω>0.设f(x)=
•
.
(Ⅰ)若a=
,b=1,ω=2,求方程f(x)=1在区间[0,π]内的解集;
(Ⅱ)根据本题条件我们可以知道,函数f(x)的性质取决于变量a、b和ω的值.当x∈R时,试写出一组a,b,ω值,使得函数f(x)满足“图象关于点(
,0)对称,且在x=
处f(x)取得最小值”.(请说明理由)
| OA |
| OB |
(Ⅰ)若a=
| 3 |
(Ⅱ)根据本题条件我们可以知道,函数f(x)的性质取决于变量a、b和ω的值.当x∈R时,试写出一组a,b,ω值,使得函数f(x)满足“图象关于点(
| π |
| 3 |
| π |
| 6 |
考点:平面向量数量积的运算,三角函数中的恒等变换应用
专题:平面向量及应用
分析:(1)由题意可得当a=
,b=1,ω=2时,由f(x)=1,可得sin(2x+
)=
,可得2x+
=2kπ+
,或2x+
=2kπ+
,k∈z.再结合x∈[0,π]求得f(x)=1在[0,2π]内的解集.
(2)由f(x)=
•
=
sin(ωx+φ),设周期 T=
.由题意可得
-
=
+
T,即ω=6n+3,n∈N,由条件求得 a=0,
=±1.再分(i)当 b>0,a=0时、(ii)当b<0 a=0时两种情况,分别求得一组a,b,ω值,从而得出结论.
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
(2)由f(x)=
| OA |
| OB |
| a2+b2 |
| 2π |
| ω |
| π |
| 3 |
| π |
| 6 |
| T |
| 4 |
| n |
| 2 |
| b |
| |b| |
解答:
解:(1)由题意可得f(x)=
•
=a•cosωx+b•sinωx,
当a=
,b=1,ω=2时,由f(x)=sin2x+
cos2x=2sin(2x+
)=1,
可得sin(2x+
)=
,2x+
=2kπ+
,k∈z,或2x+
=2kπ+
,k∈z.
求得 x=kπ-
,或 x=kπ+
,k∈z.
又因为x∈[0,π],∴2x∈[0,2π],故f(x)=1在[0,2π]内的解集为{
,
}.
(2)解:因为f(x)=
•
=
sin(ωx+φ),设周期 T=
.
由于函数f(x)须满足“图象关于点(
,0)对称,且在x=
处f(x)取得最小值”.
因此,根据三角函数的图象特征可知,
-
=
+
T,
故有
=
•
,∴ω=6n+3,n∈N,
又因为,形如f(x)=
sin(ωx+φ)的函数的图象的对称中心都是f(x)的零点,
故需满足 sin(
ω+φ)=0,而当ω=6n+3,n∈N时,
因为
(6n+3)+φ=2nπ+π+φ,n∈N;所以当且仅当φ=kπ,k∈Z时,
f(x)的图象关于点(
,0)对称;此时,
,
∴a=0,
=±1.
(i)当 b>0,a=0时,f(x)=sinωx,进一步要使x=
处f(x)取得最小值,
则有f(
)=sin(
•ω)=-1,∴
•ω=2kπ-
,故ω=12k-3,k∈z.
又ω>0,则有ω=12k-3,k∈N*;
因此,由
可得ω=12m+9,m∈N.
(ii)当b<0 a=0时,f(x)=-sinωx,进一步要使x=
处f(x)取得最小值,
则有f(
)=-sin(
•ω)=-1 (
•ω)=2kπ+
ω=12k+3 k∈z;
又ω>0,则有ω=12k+3,k∈N.
因此,由
可得ω=12m+3,m∈N.
综上,使得函数f(x)满足“图象关于点(
,0)对称,且在x=
处f(x)取得最小值
的充要条件是“b>0,a=0时,ω=12m+9,m∈N;或 当b<0 a=0时,ω=12m+3,m∈N”.
| OA |
| OB |
当a=
| 3 |
| 3 |
| π |
| 3 |
可得sin(2x+
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
求得 x=kπ-
| π |
| 12 |
| π |
| 4 |
又因为x∈[0,π],∴2x∈[0,2π],故f(x)=1在[0,2π]内的解集为{
| π |
| 4 |
| 11π |
| 12 |
(2)解:因为f(x)=
| OA |
| OB |
| a2+b2 |
| 2π |
| ω |
由于函数f(x)须满足“图象关于点(
| π |
| 3 |
| π |
| 6 |
因此,根据三角函数的图象特征可知,
| π |
| 3 |
| π |
| 6 |
| T |
| 4 |
| n |
| 2 |
故有
| π |
| 6 |
| 2π |
| ω |
| 2n+1 |
| 4 |
又因为,形如f(x)=
| a2+b2 |
故需满足 sin(
| π |
| 3 |
因为
| π |
| 3 |
f(x)的图象关于点(
| π |
| 3 |
|
∴a=0,
| b |
| |b| |
(i)当 b>0,a=0时,f(x)=sinωx,进一步要使x=
| π |
| 6 |
则有f(
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
又ω>0,则有ω=12k-3,k∈N*;
因此,由
|
(ii)当b<0 a=0时,f(x)=-sinωx,进一步要使x=
| π |
| 6 |
则有f(
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
又ω>0,则有ω=12k+3,k∈N.
因此,由
|
综上,使得函数f(x)满足“图象关于点(
| π |
| 3 |
| π |
| 6 |
的充要条件是“b>0,a=0时,ω=12m+9,m∈N;或 当b<0 a=0时,ω=12m+3,m∈N”.
点评:本题主要考查两个向量的数量积公式、三角恒等变换、正弦函数的图象的对称性,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
实数对(x,y)满足不等式组
,若目标函数z=2kx-y在x=3,y=1时取最大值,则k的取值范围是( )
|
A、(-∞,-
| ||||
B、[-
| ||||
C、[-
| ||||
D、(-∞,-
|
函数f(x)=ax2+x+1有极大值的充要条件是( )
| A、a<0 | B、a≥0 |
| C、a>0 | D、a≤0 |
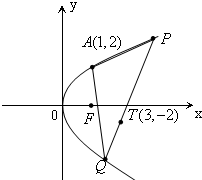 点A(1,2)到抛物线y2=2px(p>0)的焦点F的距离为2,过T(3,-2)的动直线l与此抛物线交于P、Q两点
点A(1,2)到抛物线y2=2px(p>0)的焦点F的距离为2,过T(3,-2)的动直线l与此抛物线交于P、Q两点