题目内容
已知A(-1,3),B(3,5)关于直线ax+y-b=0对称,则
= .
| a |
| b |
考点:与直线关于点、直线对称的直线方程
专题:直线与圆
分析:由对称性可得中点在直线和垂直两个关系,可得ab的方程组,解方程组可得.
解答:
解:∵A(-1,3),B(3,5)关于直线ax+y-b=0对称,
∴AB的中点(1,4)在直线ax+y-b=0上且AB连线与直线ax+y-b=0垂直,
∴a+4-b=0,且
•(-a)=-1,
解得
,∴
=
故答案为:
∴AB的中点(1,4)在直线ax+y-b=0上且AB连线与直线ax+y-b=0垂直,
∴a+4-b=0,且
| 5-3 |
| 3-(-1) |
解得
|
| a |
| b |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查直线的对称性,涉及的垂直关系和中点坐标公式,属基础题.

练习册系列答案
相关题目
数列{an}的通项公式为an=ncos
,其前n项和为Sn,则S2015等于( )
| nπ |
| 2 |
| A、1002 | B、1004 |
| C、1006 | D、-1008 |
若原点和点(1,1)都在直线x+y=a的同一侧,则a的取值范围是( )
| A、a<0或a>2 |
| B、0<a<2 |
| C、a=0或a=2 |
| D、0≤a≤2 |
如图给出的是计算
+
+
+…+
的值的一个程序框图,其中判断框中应填入的是( )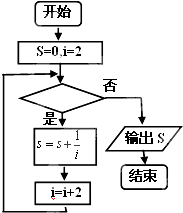
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |

| A、i>100 | B、i≤100 |
| C、i>50 | D、i≤50 |
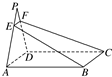 如图所示,四边形ABCD是矩形,P∉平面ABCD,过BC作平面BCFE交AP于E,交DP于F.
如图所示,四边形ABCD是矩形,P∉平面ABCD,过BC作平面BCFE交AP于E,交DP于F.
