题目内容
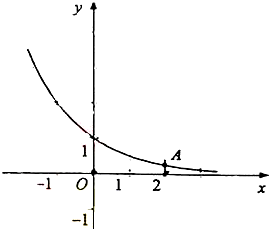 如图,函数f(x)=ax(a>0,a≠1)的图象经过点A(2,
如图,函数f(x)=ax(a>0,a≠1)的图象经过点A(2,| 1 |
| 4 |
①设x∈[0,2]时,函数y=g(x)在y=f(x)的下方,在图中画出一个符合题意的函数y=g(x)的大致图象;
对所有符合题意的函数y=g(x),写出b的取值范围
②设函数f(x)的反函数为y=f-1(x),若当x>0时,函数y=f-1(x)与y=g(x)至少要有一个函数的函数值为正实数,求b的取值范围.
考点:指数函数综合题
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:①运用代入法,求得f(x)的解析式,分别求出f(x)和g(x)在[0,2]的值域,通过图象得到
>4-2b,解出b的范围,画出一个g(x)的图象;
②求出f(x)的反函数,对x讨论,由于0<x<1时,f-1(x)>0,x≥1时,f-1(x)≤0,则对x≥1时,g(x)>0恒成立,运用参数分离和函数的单调性求出最小值,即可得到b的范围.
| 1 |
| 4 |
②求出f(x)的反函数,对x讨论,由于0<x<1时,f-1(x)>0,x≥1时,f-1(x)≤0,则对x≥1时,g(x)>0恒成立,运用参数分离和函数的单调性求出最小值,即可得到b的范围.
解答:
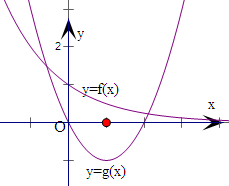 解:①函数f(x)=ax(a>0,a≠1)的图象经过
解:①函数f(x)=ax(a>0,a≠1)的图象经过
点A(2,
),则a2=
,可得a=
,即f(x)=(
)x,
g(x)=x2-bx=(x-
)2-
,由x∈[0,2]时,
函数y=g(x)的图象在y=f(x)的下方,由于b>0,
g(x)在[0,2]的范围为[-
,4-2b],f(x)在[0,2]的范围是
[
,1],则有
>4-2b,解得b>
,
即b的取值范围为(
,+∞);
②函数f(x)的反函数为y=f-1(x)=log
x,
由当x>0时,函数y=f-1(x)与y=g(x)至少要有一个函数的函数值为正实数,
由于0<x<1时,f-1(x)>0,x≥1时,f-1(x)≤0,
则对x≥1时,g(x)>0恒成立,即有x2-bx>0,
b<x对x≥1恒成立,即有0<b<1,
则b的取值范围为(0,1).
 解:①函数f(x)=ax(a>0,a≠1)的图象经过
解:①函数f(x)=ax(a>0,a≠1)的图象经过点A(2,
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
g(x)=x2-bx=(x-
| b |
| 2 |
| b2 |
| 4 |
函数y=g(x)的图象在y=f(x)的下方,由于b>0,
g(x)在[0,2]的范围为[-
| b2 |
| 4 |
[
| 1 |
| 4 |
| 1 |
| 4 |
| 15 |
| 8 |
即b的取值范围为(
| 15 |
| 8 |
②函数f(x)的反函数为y=f-1(x)=log
| 1 |
| 2 |
由当x>0时,函数y=f-1(x)与y=g(x)至少要有一个函数的函数值为正实数,
由于0<x<1时,f-1(x)>0,x≥1时,f-1(x)≤0,
则对x≥1时,g(x)>0恒成立,即有x2-bx>0,
b<x对x≥1恒成立,即有0<b<1,
则b的取值范围为(0,1).
点评:本题考查指数函数的图象和性质以及二次函数的图象和性质,主要是函数的单调性和值域,注意运用参数分离和不等式恒成立思想以及数形结合思想是解题的关键,属于中档题和易错题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目