题目内容
14.(x2-2)(1+$\frac{2}{x}$)5的展开式中x-1的系数为( )| A. | 60 | B. | 50 | C. | 40 | D. | 20 |
分析 把(1+$\frac{2}{x}$)5按照二项式定理展开,可得(x2-2)(1+$\frac{2}{x}$)5的展开式中x-1的系数.
解答 解:(x2-2)(1+$\frac{2}{x}$)5=(x2-2)[${C}_{5}^{0}$+${C}_{5}^{1}$•$\frac{2}{x}$+${C}_{5}^{2}$•${(\frac{2}{x})}^{2}$+${C}_{5}^{3}$•${(\frac{2}{x})}^{3}$+${C}_{5}^{4}$•${(\frac{2}{x})}^{4}$+${C}_{5}^{5}$•${(\frac{2}{x})}^{5}$],
故展开式中x-1的系数为23•${C}_{5}^{3}$-2•2${C}_{5}^{1}$=60,
故选:A.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,属于基础题.

练习册系列答案
相关题目
5.设集合A={x||x-2|≤2,x∈R},B={x|-1≤x≤2},则∁R(A∩B) 等于( )
| A. | {x|-1<x<0} | B. | {x|2≤x<4} | C. | {x|x<0或x>2} | D. | {x|x≤0或x≥2} |
9.“a=1”是函数f(x)=1-2sin2(ax+$\frac{π}{4}$)在区间($\frac{π}{12}$,$\frac{π}{6}$)上为减函数“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
19.命题“?x∈R,x2+2x+2>0”的否定是( )
| A. | ?x∈R,x2+2x+2≤0 | B. | ?x∈R,x2+2x+2≤0 | C. | ?x∈R,x2+2x+2<0 | D. | ?x∈R,x2+2x+2>0 |
6.将函数$f(x)=sin({2x-\frac{π}{3}})$的图象向右平移$\frac{π}{3}$个单位得到函数g(x)的图象,则g(x)的一条对称轴方程可以为( )
| A. | $x=\frac{3π}{4}$ | B. | $x=\frac{7π}{6}$ | C. | $x=\frac{7π}{12}$ | D. | $x=\frac{π}{12}$ |
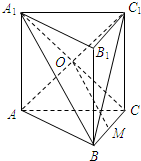 如图,已知直三棱柱ABC-A1B1C1的侧面ACC1A1是正方形,点O是侧面ACC1A1的中心,∠ACB=$\frac{π}{2}$,M是棱BC的中点.
如图,已知直三棱柱ABC-A1B1C1的侧面ACC1A1是正方形,点O是侧面ACC1A1的中心,∠ACB=$\frac{π}{2}$,M是棱BC的中点.